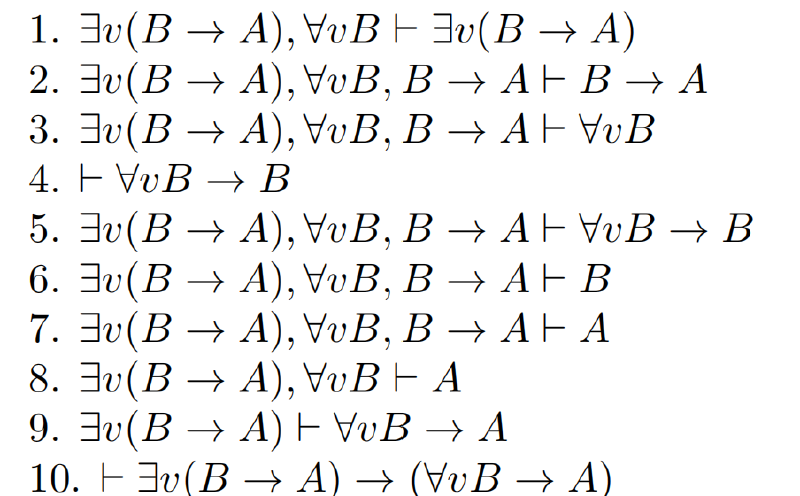FC及其相关定理

前言

水平有限，存在的错误和不足请大家指正。

本篇所述皆来自于笔者于23年学校开设的《数理逻辑》课程中讲解内容。

在先前已经给出了命题逻辑的相关介绍，但是命题逻辑存在着不可避免的缺陷，在命题逻辑中我们将原子命题看成是不可再分的基本单位，这就体现不出命题中研究对象的特性以及研究对象之间的逻辑关系，而有些推理的正确性依赖于命题的内部结构，我们以著名的苏格拉底三段论为例：

1. 所有的人都是要死的。
2. 苏格拉底是人。
3. 所以苏格拉底是要死的。

我们引入三个命题变元$P,Q,R$，我们可以写出推理的命题形式：$P\wedge Q\rightarrow R$，但是很明显这个公式并非永真式，我们不能看出原来正确的推理。 为此，我们必须引入谓词逻辑，以帮助我们研究相关的推理形式和规律。

基础知识

部分基础概念如定理、证明、演绎等在此不作赘述。

个体词：用于表示研究对象的词，分为个体常元（通常用字母表靠前的小写字母表示）和个体变元（通常用字母表靠后的小写字母表示）。

谓词：表示研究对象的性质（一个个体变元）或研究对象（多个个体变元）之间关系的词（通常用大写字母来表示）。那么我们可以得到n元谓词的概念，为了增加可读性，我们可以写作$P^{(n)}(t_1,t_2,\cdots,t_n)$。

个体域（论域）：个体变元的取值范围。

函词：用于描述从一个论域到另一个论域的映射，不难发现函词的定义类似于函数的定义，常用小写字母或小写英文单词来表示，对于含有n个个体变元的函词常记作$f^{(n)}$，为了增加可读性，我们可以写作$f^{(n)}(t_1,t_2,\cdots,t_n)$。

量词：用于限制个体词的数量，分为全称量词和存在量词。

1. 全称量词$\forall$：表任意的，从量上表示“所有的”。
2. 特称量词$\exists$：表存在的，从量上表示“至少有一个”。

在量词之间显然有着这样的对应关系：

（1）$\forall xP(x)\Leftrightarrow\neg\exists x\neg P(x)$

（2）$\exists xP(x)\Leftrightarrow\neg\forall x\neg P(x)$

（3）$\neg\forall xP(x)\Leftrightarrow\exists x\neg P(x)$

（4）$\neg\exists xP(x)\Leftrightarrow\forall x\neg P(x)$

项：类似于之前命题公式的定义，现在给出项的定义：

（1）个体变元和个体常元是项。

（2）若$f^{(n)}$是一个n元函词，且$t_1,t_2\cdots,t_n$是项，那么$f^{(n)}(t_1,t_2,\cdots,t_n)$是项。

（3）有限次的使用（1）（2）进行复合得到的结果也是项。

在此定义的项的概念在我们将介绍的FC中也是同理的。

约束变元：受量词约束的个体变元。

自由变元：不受量词约束的个体变元。

例如$\forall x(P(x,y)\rightarrow Q(x,y))\rightarrow R(x,y)$中，记前件为$A$，记后件为$B$。在前件中存在指导变元$x$，故$x$为约束变元，在后件中$x$为自由变元，在前件和后件中$y$均为自由变元。

辖域：量词所约束的范围。

合式公式：合式公式也称谓词公式，或简称公式，定义如下：

（1）不含联结词的单个谓词即原子谓词公式是合式公式。

（2）若$A$为合式公式，那么$\neg A$也是合式公式。

（3）若$A,B$为合式公式，且无变元$x$在$A,B$中的一个是约束的，而另一个是自由的，则$A\wedge B,A\vee B,A\rightarrow B,A\leftrightarrow B$都是合式公式。

（4）若$A$为合式公式，而$x$在$A$中为自由变元，则$\forall xP(x),\exists xP(X)$均为合式公式。

（5）由（1）~（4）有限次复合所形成的公式均为合式公式。

在此定义的公式的概念在我们将介绍的FC中也是同理的。

子公式：如果公式$A$为形如$wBw’$的符号串，其中$w,w’$都是符号串，$B$是公式，那么$B$就称为公式$A$的子公式。当$w,w’$中存在非空串时我们称$B$为真子公式。

易名规则：将量词辖域中出现的某个约束变元改为另一个在该辖域中未出现的个体变元，公式中的其余部分保持不变，改名后的公式称为原公式的改名式，例如$\forall xP(x)$的改名式可以是$\forall yP(x)^x_y$。在使用易名规则时需要注意待改名的变元在其辖域内的此变元都应该被改掉，而其余的保持不变，另外新引进的变元符不应该在该量词的辖域内出现。

可代入：设$v$为谓词公式$A$中的自由变元，且项$t$中不含$A$的约束变元符（若有可以使用易名规则），则称项$t$对$v$是可代入的。

例如$A=\forall v_1P(v_1,v_2)$中，若$t$不含约束变元$v$的项，那么$t$对$v_2$是可代入的。若$t=f(v_1)$，其中$f$为函词，那么$t$对$v_2$是不可代入的。

代入：对公式$A$中的自由变元$v$的所有自由出现都换为项$t$（必须是可代入的），记为$A^v_t$。若$A$中无$v$的出现则$A^v_t=A$。值得注意的是：我们使用记号$A^{v_1,v_2,\cdots,v_n}{t_1,t_2,\cdots,t_n}$表示对$A$的变元$v_1,v_2,\cdots,v_n$同时做代入，即将$v_i$代为$t_i$，而不同于$(\cdots((A^{v_1}{t_1})^{v_2}{t_2})^{v_3}{t_3}\cdots)^{v_n}_{t_n}$。

全称化：设$v_1,v_2,\cdots,v_n$为公式$A$中的自由变元，则公式$\forall v_{i_1}\forall v_{i_2}\cdots\forall v_{i_r}A$称为$A$的全称化，其中$1\leq i_1,i_2,\cdots,i_r\leq n,1\leq r\leq n$。当$r=n$时即为$A$的全称封闭式。

有了这些基础知识后，我们便可以将自然语句形式化，例如：

命题“过平面上两个不同点有且仅有一条直线通过”，令：

谓词$D(x)$表示：$x$为平面上的点

谓词$G(x)$表示：$x$为平面上的直线

谓词$L(x,y,z)$表示：$z$通过$x,y$

谓词$E(x,y)$表示：$x$与$y$相等

那么我们可以将语句形式化为：

$\forall x\forall y(D(x)\wedge D(y)\wedge\neg E(x,y)\rightarrow \exists z(G(z)\wedge L(x,y,z)\wedge\forall u(G(u)\wedge L(x,y,u)\rightarrow E(u,z))))$

一阶谓词形式系统的语义

个体常元、变元、项、函词、谓词等属于语法范畴的概念，它们只是一些字符串，并不具备实际意义。为了讨论谓词演算公式的真值，就需要对函词、谓词进行指称，对个体常元、变元取值的指派，即赋予它们一定的意义。

在一阶谓词演算系统中，证明和推演只是公式符号组合的形式变糊，并未考虑到其语义，但是建立一个形式系统正是为了研究正确的逻辑推理形式及其规律，为此，在予以解释后，其中的公理和定理应当是逻辑规律的反映。

由于相较于命题逻辑我们引入了谓词、函词、量词等符号，对谓词公式的解释会更加复杂，其语义解释通常是一个数学结构，包括论域$D$及对常元、函词、谓词进行指称的解释$I$，我们得到了一个结构$U=< D,I >$，全体结构的集合记为$T$（这样的结构通常称为$Tarski$语义类）。

解释I的组成

一个解释就是一个映射$I$，它指称常元、函词和谓词为：

（1）对任一常元$a$指定为论域$D$的一个个体，记为$I(a)$，简记为$\overline{a}$。

（2）对每一n元函词$f^{(n)}$指定为$D$上的一个n元函数，记为$I(f^{(n)})$，简记为$\overline{f}^{(n)}$。

（3）对每一n元谓词$P^{(n)}$指定为$D$上的一个n元关系，记为$I(P^{(n)})$，简记为$\overline{P}^{(n)}$。

指派

一阶谓词演算中的指派是对个体变元指定为论域$D$中的个体作为其取值，即为映射$s:${$v_1,v_2,\cdots$}$\rightarrow D$。即对任一变元$v_i,s(v_i)\in D$。

指派$s$可以扩展为从项集合到个体域的映射$\overline{s}$：对于任意的项$t$，

（1）$\overline{s}(t)=s(v)$，当$t$为变元$v$时。

（2）$\overline{s}(t)=\overline{a}$，当$t$为常元$a$时。

（3）$\overline{s}(t)=\overline{f}^{(n)}(\overline{s}(t_1),\overline{s}(t_2),\cdots,\overline{s}(t_n))$，当$t$为n元函词$f^{(n)}(t_1,t_2,\cdots,t_n)$时。

不难发现指派$s$域解释$I$是相互独立的，但是指派$\overline{s}$却是依赖于解释$I$的。

有了结构$U=< D,I >$及指派$s$，于是对公式$A$在结构$U=< D,I >$及指派$s$下取值为真记为$\models_UA[s]$，反之记为$\nvDash_UA[s]$。而$\models_UA$则表示在结构$U$中对一切可能的指派$s$，公式$A$皆为真；而$\models A$或者$\models_TA$表示公式$A$在一切结构$U$中均为真，即$A$永真。

$\models_UA[s]$的严格定义

除了解释和指派，我们还需要对量词和联结词的意义作出规定，为此我们给出递归定义来明确$\models_UA[s]$的严格定义。

（1）当$A$为原子公式$P^{(n)}(t_1,\cdots,t_n)$时$\models_UA[s]$当且仅当$< \overline{s}(t_1),\cdots,\overline{s}(t_n) >\in\overline{P}^{(n)}$，即此时n元谓词所描述的n元关系成立。

（2）当$A$为公式$\neg B$时$\models_UA[s]$当且仅当$\nvDash_UB[s]$。

（3）当$A$为公式$B\rightarrow C$时$\models_UA[s]$当且仅当$\nvDash_UB[s]$或$\models_UC[s]$。

（4）当$A$为公式$\forall vB$时$\models_UA[s]$当且仅当对每一个$d\in D$都有$\models_UB[s(v|d)]$，其中指派$s(v|d)$表示除了对变元$v$用指定元素$d$赋值外，对其他变元的指派与$s$相同。

当我们使用联结词$\vee,\wedge$和存在量词$\exists$时可以补充：

（1）$\models_UB\vee C[s]$当且仅当$\models_UB[s]$或$\models_UC[s]$。

（2）$\models_UB\wedge C[s]$当且仅当$\models_UB[s]$且$\models_UC[s]$。

（3）$\models_U\exists vB[s]$当且仅当存在$d\in D$使得$\models_UB[s(v|d)]$。

一阶谓词演算形式系统FC的简单介绍

一阶谓词演算形式系统FC（First order predicate Calculus）是一种形式系统，我们先简单介绍一下FC的组成部分：

1. 字母表$\Sigma=L_v\cup L_a\cup L_f\cup L_p\cup L_l$，其中$L_v$即个体变元，$L_a$即个体常元，$L_f$即各种函词，$L_p$即各种谓词，$L_l$包括了真值联结词$\rightarrow,\neg$，量词$\forall$和括号$(,)$。

   （1）在这里其他的联结词和存在量词$\exists$都被视作是缩写符号。

   （2）这里的介绍中未引入等词$=$。

   （3）$L_f=\varnothing$时称之为纯谓词演算系统。

   （4）如果我们引入0元谓词符号，那么实际上我们就得到了PC，故可以将PC视作FC的子系统，在PC中成立的定理可以迁移到FC中。

2. 形式规则：上文提到的合式公式的定义

3. 公理：设$A,B,C$为代表FC中任意公式的语法变元，$v$为任意变元，$t$为任意项，那么FC中有六个公理模式 $A1:A\rightarrow (B\rightarrow A)$ $A2:(A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$ $A3:(\neg A\rightarrow\neg B)\rightarrow (B\rightarrow A)$ $A4:\forall vA\rightarrow A^v_t$，若$t$对$A$中的变元$v$可代入 $A5:\forall v(A\rightarrow B)\rightarrow(\forall vA\rightarrow\forall vB)$ $A6:A\rightarrow\forall vA$，若$v$在$A$中无自由出现 FC的公理包含上述六个公理模式和他们对应的全称化，同时后面的3个公理也是永真式，在此不作证明。

4. 推理规则：同PC中的规则$r_{mp}$：即若有$A$和$A\rightarrow B$成立，那么$B$也成立，形式化的推理序列为：$A,A\rightarrow B,B$。 可以记作$\displaystyle{\frac{A,A\rightarrow B}{B}}$

FC是完备的，也就是说所有永真式均为FC的定理，$G\ddot{o}del$首先发现并证明了这一事实，即$G\ddot{o}del$完备性定理。

FC中的基本定理

FC的定理

下列总结了FC中12个基本定理，并给出了部分证明：

$Th1$：对于FC中的任何公式$A$和变元$v$，$\vdash_{FC}\forall vA\rightarrow A$

1. $\forall vA\rightarrow A^v_v$,$A4$，后者即$A$

$Th2$：对于FC中的任何公式$A$和变元$v$，$\vdash_{FC}A\rightarrow\neg\forall v\neg A$，即$\vdash_{FC}A\rightarrow\exists vA$

1. $\forall v\neg A\rightarrow\neg A$,$A4$
2. $(\forall v\neg A\rightarrow\neg A)\rightarrow(A\rightarrow\neg\forall v\neg A)$,$PC$中的定理
3. $A\rightarrow\neg\forall v\neg A$,$r_{mp}(1)(2)$

$Th3$：对于FC中的任何公式$A$和变元$v$，$\vdash_{FC}\forall vA\rightarrow\exists vA$

1. $\forall vA\rightarrow A$,$Th1$
2. $A\rightarrow\exists vA$,$Th2$
3. $\forall vA\rightarrow\exists vA$,三段论

$Th4$：（普化定理/全称推广定理）对于FC中的任何公式$A$和变元$v$，如果$\vdash_{FC}A$，那么$\vdash_{FC}\forall vA$ 需要注意的是$\vdash_{FC}A\rightarrow\forall vA$并不一定成立，故在$A6$中我们作出了额外的要求：$v$在$A$中无自由出现。

证明：设$A_1,A_2,\cdots,A_n(=A)$是FC中公式$A$的证明序列，对证明的长度n使用归纳法。 （1）当n=1时，$A$只能是公理。若$v$在$A$中自由出现，那么$\forall vA$也是公理；若$v$不在$A$中自由出现，则$A\rightarrow\forall vA$为公理，由$r_{mp}$知$\forall vA$为公理。 （2）当n>1时，若$A$为公理，仿照（1）的证明可知$\forall vA$为定理。若$A_n$为$A_j(i< n)$，则由归纳假设可知$\forall vA_j=\forall vA$为定理。若$A_n$是由$A_i,A_j$通过$r_{mp}$推得，不妨设$A_j=A_i\rightarrow A$，则由归纳假设$\forall vA_i,\forall v(A_i\rightarrow A)$都是定理。再由公理$\forall v(A_i\rightarrow A)\rightarrow(\forall vA_i\rightarrow\forall vA)$知$\forall vA_i\rightarrow\forall vA$为定理，使用$r_{mp}$则知$\forall vA$为定理。

$Th5$：对于FC中的任何公式集合$\Gamma$，公式$A$和不在$\Gamma$的任意公式中自由出现的变元$v$，对$Th4$进行推广，得到：如果$\Gamma\vdash_{FC}A$，那么$\Gamma\vdash_{FC}\forall vA$。

证明：设$A_1,A_2,\cdots,A_n(=A)$是FC中公式$A$的演绎序列，对证明的长度n使用归纳法。 （1）当n=1时，若$A$是公理。若$v$在$A$中自由出现，那么$\forall vA$也是公理；若$v$不在$A$中自由出现，则$A\rightarrow\forall vA$为公理，由$r_{mp}$知$\forall vA$为公理。于是当$A$为公理时，都有$\Gamma\vdash\forall vA$。若$A\in\Gamma$，则$v$不在$A$中自由出现，从而$A\rightarrow\forall vA$为公理，从而由$r_{mp}$知$\Gamma\vdash\forall vA$。 （2）当n>1时，若$A$为公理或者$A\in\Gamma$，仿照（1）的证明可知$\forall vA$为定理。若$A_n$为$A_j(i< n)$，则由归纳假设可知$\forall vA_j=\forall vA$为定理。若$A_n$是由$A_i,A_j$通过$r_{mp}$推得，不妨设$A_j=A_i\rightarrow A$，则由归纳假设$\forall vA_i,\forall v(A_i\rightarrow A)$都是定理。再由公理$\forall v(A_i\rightarrow A)\rightarrow(\forall vA_i\rightarrow\forall vA)$知$\forall vA_i\rightarrow\forall vA$为定理，使用$r_{mp}$则知$\forall vA$为定理。

$Th6$：（演绎定理）在FC中演绎定理也成立，对于FC中任何公式集合$\Gamma$和FC中的任意两个公式$A,B$，那么$\Gamma;A\vdash_{FC}B$当且仅当$\Gamma\vdash_{FC}A\rightarrow B$。

证明：类似于在PC中演绎定理的证明，在此不作说明。

$Th7$：设$\Gamma$为FC中的任一公式集合，$A,B$为FC中任意两个公式，$\Gamma;A\vdash_{FC}\neg B$当且仅当$\Gamma;B\vdash_{FC}\neg A$。

1. $\Gamma;A\vdash\neg B$
2. $\Gamma\vdash A\rightarrow\neg B$,$Th6$
3. $\Gamma\vdash(A\rightarrow\neg B)\rightarrow(B\rightarrow\neg A)$,$PC$中的定理
4. $\Gamma\vdash B\rightarrow\neg A$,$r_{mp}(2)(3)$
5. $\Gamma;B\vdash\neg A$,$Th6$

$Th8$：（反证法）如果FC中的公式集合$\Gamma\cup${$A$}是不一致的，则$\Gamma\vdash_{FC}\neg A$。

证明：由于$\Gamma\cup${$A$}不一致，则存在公式$B$使得$\Gamma;A\vdash B$和$\Gamma;A\vdash\neg B$。由于$\neg B\rightarrow(B\rightarrow\neg A)$为定理，所以$\Gamma;A\vdash\neg A$，由演绎定理得$\Gamma\vdash A\rightarrow\neg A$，又因为$(A\rightarrow\neg A)\rightarrow\neg A$为定理，从而$\Gamma\vdash\neg A$。

$Th9$：设$\Gamma$为FC中的任一公式集合，$A,B$为FC中的任意两个公式，并且变元$v$不在$\Gamma$的任何公式里面自由出现，那么$\Gamma;A\vdash_{FC}B$蕴含$\Gamma;\forall vA\vdash_{FC}B$和$\Gamma;\forall vA\vdash_{FC}\forall vB$。

1. $\Gamma;A\vdash B$
2. $\Gamma\vdash A\rightarrow B$,$Th6$
3. $\Gamma\vdash\forall v(A\rightarrow B)$,$Th4$
4. $\Gamma\vdash\forall v(A\rightarrow B)\rightarrow(\forall vA\rightarrow\forall vB)$,$A5$
5. $\Gamma\vdash\forall vA\rightarrow\forall vB$,$r_{mp}(3)(4)$
6. $\Gamma;\forall vA\vdash\forall vB$,$Th6$
7. $\Gamma;\forall vA\vdash B$,$Th1$

$Th10$：（存在消除）设$\Gamma$为FC中的任一公式集合，$A,B$为FC中的任意两个公式，并且变元$v$不在$\Gamma$的任何公式以及公式$B$里面自由出现，那么由$\Gamma\vdash_{FC}\exists vA$以及$\Gamma;A\vdash_{FC}B$可以推出$\Gamma\vdash_{FC}B$。

1. $\Gamma;A\vdash B$
2. $\Gamma\vdash A\rightarrow B$
3. $\Gamma\vdash(A\rightarrow B)\rightarrow(\neg B\rightarrow A)$,$PC$中的定理
4. $\Gamma\vdash\neg B\rightarrow\neg A$,$r_{mp}(2)(3)$
5. $\Gamma\vdash;\neg B\vdash\neg A$
6. $\Gamma;\neg B\vdash\forall v\neg A$,$Th2$
7. $\Gamma\vdash\neg B\rightarrow\forall v\neg A$
8. $\Gamma\vdash(\neg B\rightarrow\forall v\neg A)\rightarrow(\neg\forall v\neg A\rightarrow B)$,$PC$中的定理
9. $\Gamma\vdash\neg\forall v\neg A\rightarrow B$,$r_{mp}(7)(8)$
10. $\Gamma\vdash\exists vA\rightarrow B$
11. $\Gamma\vdash\exists vA$
12. $\Gamma\vdash B$,$r_{mp}(10)(11)$

$Th11$：（替换原理）设$A,B$为FC的公式，且满足$A\vdash\dashv_{FC}B$，$A$是$C$的子公式，$D$是将$C$中$A$的若干出现换为公式$B$得到的公式，则$C\vdash\dashv_{FC}D$。

证明：略

$Th12$：（改名定理）在FC中若$A’$是$A$的改名式，且$A’$改用的变元不在$A$中出现，则$A\vdash\dashv_{FC}A’$。

证明：略

例题

证明：$\vdash A\rightarrow B$且变元$v$在$B$中无自由出现，则$\vdash\exists vA\rightarrow B$。

1. $\vdash A\rightarrow B$
2. $\vdash\neg B\rightarrow\neg A$,$PC$中的定理
3. $\vdash\forall v(\neg B\rightarrow\neg A)$,$Th1$
4. $\vdash\forall v(\neg B\rightarrow\neg A)\rightarrow(\forall v\neg B\rightarrow\forall v\neg A)$,$A5$
5. $\vdash\forall v\neg B\rightarrow\forall v\neg A$,$r_{mp}(3)(4)$
6. $\vdash\neg B\rightarrow\forall v\neg B$,$A6$
7. $\vdash\neg B\rightarrow\forall v\neg A$,三段论
8. $\vdash(\neg B\rightarrow\forall v\neg A)\rightarrow(\neg\forall v\neg A\rightarrow B)$,$PC$中的定理
9. $\vdash\neg\forall v\neg A\rightarrow B$,$r_{mp}(7)(8)$

证明：$\vdash(A\rightarrow\exists vB)\rightarrow\exists v(A\rightarrow B)$，其中$v$在$A$中无自由出现。

1. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\forall v\neg(A\rightarrow B)$
2. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\neg(A\rightarrow B)$,$Th1$
3. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\neg(A\rightarrow B)\rightarrow\neg B$,$PC$中的定理
4. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\neg B$,$r_{mp}(2)(3)$
5. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\forall v\neg B$,$Th1$
6. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\neg(A\rightarrow B)\rightarrow A$,$PC$中的定理
7. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash A$,$r_{mp}(2)(6)$
8. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash A\rightarrow\exists vB$
9. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\exists vB$,$r_{mp}(7)(8)$
10. $A\rightarrow\exists vB,\forall v\neg(A\rightarrow B)\vdash\neg\forall v\neg B$
11. $A\rightarrow\exists vB\vdash\neg\forall v\neg(A\rightarrow B)$,对(5)和(10)使用反证法
12. $A\rightarrow\exists vB\vdash\exists v(A\rightarrow B)$
13. $\vdash(A\rightarrow\exists vB)\rightarrow\exists v(A\rightarrow B)$

其他形式的一阶谓词演算系统

FC的形式是简洁的，但是正如PC所具有的问题那样，在实际应用中FC并不方便，因为它所使用的联结词、量词和公理数量太少了。故类似于先前在介绍完PC后引入了ND，本文将引入FCM和FND两个形式系统，以便让我们的推理更加直观。

FCM形式系统

FCM形式系统是由莫绍揆教授提出的使用五个逻辑联结词（$\neg,\rightarrow,\vee,\wedge,\leftrightarrow$）和两个量词（$\forall,\exists$）的一阶谓词演算形式系统：

1. 公理：设$A,B,C$为代表FC中任意公式的语法变元，$v$为任意变元，$t$为任意项，那么FCM的公理包含下列七组公理模式及其对应的全称化

   $A1.1:A\rightarrow A$

   $A1.2:(A\rightarrow(B\rightarrow C))\rightarrow(B\rightarrow(A\rightarrow C))$

   $A1.3:(A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$

   $A1.4:(A\rightarrow(A\rightarrow B))\rightarrow(A\rightarrow B)$

   $A2.1:(A\leftrightarrow B)\rightarrow(A\rightarrow B)$

   $A2.2:(A\leftrightarrow B)\rightarrow(B\rightarrow A)$

   $A2.3:(A\rightarrow B)\rightarrow((B\rightarrow A)\rightarrow(A\leftrightarrow B))$

   $A3.1:A\rightarrow(A\vee B)$

   $A3.2:B\rightarrow(A\vee B)$

   $A3.3:(A\rightarrow C)\rightarrow((B\rightarrow C)\rightarrow(A\vee B\rightarrow C))$

   $A4.1:A\wedge B\rightarrow A$

   $A4.2:A\wedge B\rightarrow B$

   $A4.3:A\rightarrow(B\rightarrow A\wedge B)$

   $A5.1:(A\rightarrow\neg B)\rightarrow(B\rightarrow\neg A)$

   $A5.2:\neg\neg A\rightarrow A$

   $A6.1:\forall vA\rightarrow A^v_t$，若$t$对$A$中的变元$v$可代入

   $A6.2:\forall v(A\rightarrow B)\rightarrow(\forall vA\rightarrow\forall vB)$

   $A6.3:A\rightarrow\forall vA$，若$v$在$A$中无自由出现

   $A7.1:\exists vA\rightarrow\neg\forall v\neg A$

   $A7.2:\neg\forall v\neg A\rightarrow\exists vA$

   这七组公理模式是显然的，很多在之前已经进行了证明。

2. 推理规则：$r_{mp}$

FND形式系统

在ND的基础上，很容易扩展出一个谓词演算的自然推理系统，我们称作FND，FND在ND的基础上新增添了一些规则，主要是增加了有关量词的推理规则，其余规则保持不变。

1. $\forall$引入规则${\frac{\Gamma\vdash A}{\Gamma\vdash\forall vA}}(\forall+)$
2. $\forall$消除规则${\frac{\Gamma\vdash\forall vA}{\Gamma\vdash A^v_t}}(\forall-)$，若$t$对$A$中的变元$v$可代入
3. $\exists$引入规则${\frac{\Gamma\vdash A^t_t}{\Gamma\vdash\exists vA}}(\exists+)$，若$t$对$A$中的变元$v$可代入
4. $\exists$消除规则${\frac{\Gamma\vdash\exists vA,\Gamma;A^v_t\vdash B}{\Gamma\vdash B}}(\exists-)$，其中常元$c$在$\Gamma$及公式$A,B$中均无自由出现

我们现在对这里的推理规则的意义进行解释：

1. $(\forall+)$规则：考虑FC中的全称引入定理。
2. $(\forall-)$规则：考虑FC的公理$\forall vA\rightarrow A^v_t$，若$t$对$A$中的变元$v$可代入。
3. $(\exists+)$规则：考虑FC的定理$A^v_t\rightarrow\exists vA$，若$t$对$A$中的变元$v$可代入。
4. $(\exists-)$规则：考虑FC的存在消除定理。

例题

证明：$\exists x(A\vee B)\vdash\dashv\exists xA\vee\exists xB$

1. $\exists x(A\vee B),A\vee B,A\vdash A$,$(\in)$
2. $\exists x(A\vee B),A\vee B,A\vdash\exists xA$,$(\exists+)(1)$
3. $\exists x(A\vee B),A\vee B,A\vdash\exists xA\vee\exists xB$,$(\vee+)(2)$
4. $\exists x(A\vee B),A\vee B,B\vdash B$,$(\in)$
5. $\exists x(A\vee B),A\vee B,B\vdash\exists xB$,$(\exists+)(4)$
6. $\exists x(A\vee B),A\vee B,B\vdash\exists xA\vee\exists xB$,$(\vee+)(5)$
7. $\exists x(A\vee B),A\vee B\vdash A\vee B$,$(\in)$
8. $\exists x(A\vee B),A\vee B\vdash\exists xA\vee\exists xB$,$(\vee-)(3)(6)(7)$
9. $\exists x(A\vee B)\vdash\exists x(A\vee B)$,$(\in)$
10. $\exists x(A\vee B)\vdash\exists xA\vee\exists xB$,$(\exists-)(8)(9)$
11. $\exists xA\vee\exists xB,\exists xA,A\vdash A$,$(\in)$
12. $\exists xA\vee\exists xB,\exists xA,A\vdash A\vee B$,$(\vee+)(11)$
13. $\exists xA\vee\exists xB,\exists xA,A\vdash\exists x(A\vee B)$,$(\exists+)(12)$
14. $\exists xA\vee\exists xB,\exists xA\vdash\exists xA$,$(\in)$
15. $\exists xA\vee\exists xB,\exists xA\vdash\exists x(A\vee B)$,$(\exists-)(13)(14)$
16. $\exists xA\vee\exists xB,\exists xB,B\vdash B$,$(\in)$
17. $\exists xA\vee\exists xB,\exists xB,B\vdash A\vee B$,$(\vee+)(16)$
18. $\exists xA\vee\exists xB,\exists xB,B\vdash\exists x(A\vee B)$,$(\exists+)(17)$
19. $\exists xA\vee\exists xB,\exists xB\vdash\exists xB$,$(\in)$
20. $\exists xA\vee\exists xB,\exists xB\vdash\exists x(A\vee B)$,$(\exists-)(18)(19)$
21. $\exists xA\vee\exists xB\vdash\exists xA\vee\exists xB$,$(\in)$
22. $\exists xA\vee\exists xB\vdash\exists x(A\vee B)$,$(\vee-)(15)(20)(21)$
23. $\exists x(A\vee B)\vdash\dashv\exists xA\vee\exists xB$

FC定理证明习题选

下面给出了八道FC定理习题供读者练习使用：

1. 证明：$\forall x(A\rightarrow B)\vdash A\rightarrow\forall xB$，其中$x$在$A$中无自由出现。
2. 证明: $\vdash\exists v(A\rightarrow B)\rightarrow(A\rightarrow\exists vB)$，其中$v$在$A$中无自由出现。
3. 证明：存在一种方法能击败所有敌人，那么所有敌人都存在一种方法让其被击败。
4. 证明：$\exists x(A\wedge B)\vdash\exists xA\wedge\exists xB$
5. 证明：$\Gamma=${$\exists x(P(x)\wedge\forall y(D(y)\rightarrow L(x,y))),\forall x\forall y(P(x)\wedge Q(y)\rightarrow\neg L(x,y))$}，则有$\Gamma\vdash\forall y(D(y)\rightarrow\neg Q(y))$。
6. 证明：$\Gamma=${$P(Sam),G(Clyde)\wedge L(Clyde,Oscar),(P(Oscar)\oplus G(Oscar))\wedge L(Oscar,Sam)$}，则有$\Gamma\vdash\exists x\exists y(G(x)\wedge P(y)\wedge L(x,y))$，注：$\oplus$表示联结词中的“异或”。
7. 证明：$\Gamma=${$\forall x(N(x)\rightarrow E(x)\oplus O(x)),\forall x(N(x)\rightarrow(E(x)\leftrightarrow G(x))),\neg\forall x(N(x)\rightarrow G(x))$}，则有$\Gamma\vdash\exists x(N(x)\wedge O(x))$。
8. 证明：有二元关系$R$，若$R$是传递且反自反的，那么它是非对称的。