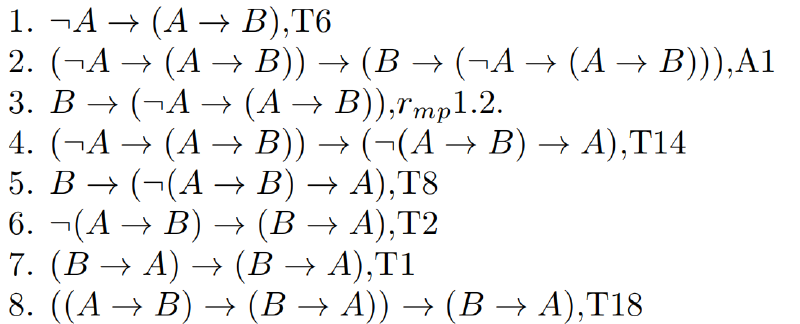PC及其相关定理

前言

水平有限，存在的错误和不足请大家指正。

本篇所述皆来自于笔者于23年学校开设的《数理逻辑》课程中讲解内容。

基础知识

命题：能唯一确定真假值的陈述句。

原子命题：不能分解为更简单的陈述句的命题。

复合命题：由联结词及简单命题构成的命题。

命题变元：用来表示命题的英文字母。（下列的$A,B$为命题变元）

联结词：有五种常用的联结词，如下所示。

1. 否定词$\neg$：表示“非”，如$\neg A$表示“对$A$的否定”。
2. 合取词$\wedge$：表示“与”，如$A\wedge B$表示“$A$与$B$”。
3. 析取词$\vee$：表示“或”，如$A\vee B$表示“$A$或$B$”。
4. 蕴涵词$\rightarrow$：表示“如果……那么”，如$A\rightarrow B$表示“如果$A$，那么$B$”，其中$A$被称为前件，$B$被称为后件。
5. 双条件词$\leftrightarrow$：表示“当且仅当”，如$A\leftrightarrow B$表示“$A$当且仅当$B$”。

为表示方便，我们约定联结词的运算优先级从高到低为$\neg,(\wedge,\vee),\rightarrow,\leftrightarrow$

命题公式的定义：

（1）原子命题是命题公式。

（2）若$A,B$是命题公式，那么$\neg A,A\wedge B,A\vee B,A\rightarrow B,A\leftrightarrow B$也是命题公式。

（3）有限次的使用（1）（2）进行复合得到的结果也是命题公式。

命题逻辑演算形式系统PC的简单介绍

命题逻辑演算形式系统PC（propositional calculus）是一种形式系统，我们先简单介绍一下PC的组成部分：

1. 字符集：包括原子变元符$p_1,p_2,\cdots,p_n,\cdots$、联结词完备集{$\neg,\rightarrow$}、辅助符号$(,)$

2. 形成规则：由原子变元符及联结词形成命题公式的规则，即上文提到的命题公式的定义

3. 公理：设$A,B,C$为可以表达任意命题公式的语法变元，那么PC中有三个公理 $A1:A\rightarrow (B\rightarrow A)$

   $A2:(A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$

   $A3:(\neg A\rightarrow\neg B)\rightarrow (B\rightarrow A)$

   $A1$的含义是：如果$A$成立，那么已知$B$成立的前提下$A$任旧成立。

   $A2$的含义是：如果$A$成立能使得只需要$B$成立那么$C$就会成立，那么如果$A$能推出$B$、$A$就能推出$C$。

   $A3$的含义是：如果$A$不成立能推出$B$不成立，那么$B$成立就能推出$A$成立。

4. 推理规则：用于从已有的公理和已推出的结论来推理另一结论。 在PC中只有分离规则$r_{mp}$：即若有$A$和$A\rightarrow B$成立，那么$B$也成立，形式化的推理序列为：$A,A\rightarrow B,B$。 可以记作$\displaystyle{\frac{A,A\rightarrow B}{B}}$

5. 定理推导：包括所有的推理结论及其推理过程。

逻辑推理相关的基本定义

1. 证明：称以下公式序列为公式$A$在PC中的一个证明：$A_1,A_2,\cdots,A_{m-1},A$，其中$A_i$或为PC的公理、或为$A_j(j< i)$、或为$A_j,A_k(j,k< i)$通过形成规则得到的。
2. 定理：公式$A$在PC中有一个证明序列，那么它就是PC的定理，我们记为$\vdash_{PC}A$。
3. 演绎：设$\Gamma$为PC中若干公式构成的公式集，则称下列公式序列为公式$A$以$\Gamma$为前提的演绎：$A_1,A_2,\cdots,A_{m-1},A$，其中$A_i$或为PC的公理、或为$\Gamma$中的成员、或为$A_j(j< i)$、或为$A_j,A_k(j,k< i)$通过分离规则得到的。我们可以记为$\Gamma\vdash_{PC}A$。

例：证明$A\vdash_{PC}B\rightarrow A$（这个定理说明了我们对一个定理增添前件后任旧是一个定理）。也就是说我们已经知道$A$成立了，现在要推出$B\rightarrow A$也成立，这个过程都要在PC中进行，故我们要在PC中构造一个演绎序列使得最后一个公式是$B\rightarrow A$，一个可行的公式序列如下：

1. $A$ （$A$是演绎前提中的成员）
2. $A\rightarrow(B\rightarrow A)$,$A1$ （$A\rightarrow(B\rightarrow A)$是公理中的$A1$）
3. $B\rightarrow A$,$r_{mp}(1)(2)$ （对公式序列中的$(1)(2)$使用分离规则得到结论$B\rightarrow A$）

上面我们成功构造了一个符合演绎要求的公式序列，也就是说有$A\vdash_{PC}B\rightarrow A$，我们完成了这个例子的证明。

实际上我们可以证明PC有合理性、一致性、完备性，这表明PC中的定理是永真的、从$\Gamma$演绎出$A$就会有$\Gamma\Rightarrow A$（合理性），PC不会推出相互矛盾的结论（一致性），任何PC中的永真式都是PC的定理（完备性）。

PC的基本定理

在PC中直接使用公理和推理规则得出PC中的定理会非常繁琐，其中有不少步骤遵循相同的模式，下列总结了PC中35个基本定理（其中7个定理较为重要），用于帮助寻找PC的定理：

$Th1$：$\vdash_{PC}A\rightarrow A$

1. $A\rightarrow(B\rightarrow A)$,$A1$
2. $A\rightarrow((B\rightarrow A)\rightarrow A)$,$A1$
3. $(A\rightarrow((B\rightarrow A)\rightarrow A))\rightarrow((A\rightarrow(B\rightarrow A))\rightarrow(A\rightarrow A))$,$A2$
4. $(A\rightarrow(B\rightarrow A))\rightarrow(A\rightarrow A)$,$r_{mp}(2)(3)$
5. $A\rightarrow A$,$r_{mp}(1)(4)$

前件互换定理

$Th2$：若$\vdash_{PC}A\rightarrow(B\rightarrow C)$，则$\vdash_{PC}B\rightarrow(A\rightarrow C)$

1. $A\rightarrow(B\rightarrow C)$
2. $(A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$A2$
3. $(A\rightarrow B)\rightarrow(A\rightarrow C)$,$r_{mp}(1)(2)$
4. $((A\rightarrow B)\rightarrow(A\rightarrow C))\rightarrow(B\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C)))$,$A1$
5. $B\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$r_{mp}(3)(4)$
6. $(B\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C)))\rightarrow((B\rightarrow(A\rightarrow B))\rightarrow(B\rightarrow(A\rightarrow C)))$,$A2$
7. $(B\rightarrow(A\rightarrow B))\rightarrow(B\rightarrow(A\rightarrow C))$,$r_{mp}(5)(6)$
8. $B\rightarrow(A\rightarrow B)$,$A1$
9. $B\rightarrow(A\rightarrow C)$,$r_{mp}(7)(8)$

$Th3$：$\vdash_{PC}(A\rightarrow(B\rightarrow C))\rightarrow(B\rightarrow(A\rightarrow C))$

1. $(A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$A1$
2. $(A\rightarrow B)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C))$,$Th2$（因为这是PC中的一个定理，所以它存在一个对应的证明序列，这里实际上是一种简写，不将这个定理对应的证明序列写出，后续的证明中我们也这样简写）
3. $((A\rightarrow B)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C)))\rightarrow(B\rightarrow((A\rightarrow B)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C))))$,$A1$
4. $B\rightarrow((A\rightarrow B)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C)))$,$r_{mp}(2)(3)$
5. $(B\rightarrow((A\rightarrow B)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C))))\rightarrow((B\rightarrow(A\rightarrow B))\rightarrow(B\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C))))$,$A2$
6. $(B\rightarrow(A\rightarrow B))\rightarrow(B\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C)))$,$r_{mp}(4)(5)$
7. $B\rightarrow(A\rightarrow B)$,$A1$
8. $B\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow(A\rightarrow C))$,$r_{mp}(6)(7)$
9. $(A\rightarrow (B\rightarrow C))\rightarrow(B\rightarrow(A\rightarrow C))$,$Th2$

加前件定理

$Th4$：$\vdash_{PC}(B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$

1. $(A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$A2$
2. $((A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C)))\rightarrow((B\rightarrow C)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))))$,$A1$
3. $(B\rightarrow C)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C)))$,$r_{mp}(1)(2)$
4. $((B\rightarrow C)\rightarrow((A\rightarrow (B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))))\rightarrow(((B\rightarrow C)\rightarrow((A\rightarrow (B\rightarrow C))))\rightarrow((B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))))$,$A2$
5. $((B\rightarrow C)\rightarrow((A\rightarrow (B\rightarrow C))))\rightarrow((B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C)))$,$r_{mp}(3)(4)$
6. $(B\rightarrow C)\rightarrow((A\rightarrow (B\rightarrow C)))$,$A1$
7. $(B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$r_{mp}(5)(6)$

加后件定理

$Th5$：$\vdash_{PC}(A\rightarrow B)\rightarrow((B\rightarrow C)\rightarrow(A\rightarrow C))$

1. $(B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$Th4$
2. $(A\rightarrow B)\rightarrow((B\rightarrow C)\rightarrow(A\rightarrow C))$,$Th2$

三段论定理

$Th6$：$\vdash_{PC}A\rightarrow B,\vdash_{PC}B\rightarrow C$，那么$\vdash_{PC}A\rightarrow C$

1. $(B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$Th4$
2. $B\rightarrow C$
3. $(A\rightarrow B)\rightarrow(A\rightarrow C)$,$r_{mp}(1)(2)$
4. $A\rightarrow B$
5. $A\rightarrow C$,$r_{mp}(3)(4)$

$Th7$：$\vdash_{PC}\neg A\rightarrow (A\rightarrow B)$

1. $\neg A\rightarrow(\neg B\rightarrow\neg A)$,$A1$
2. $(\neg B\rightarrow\neg A)\rightarrow (A\rightarrow B)$,$A3$
3. $\neg A\rightarrow(A\rightarrow B)$,$Th6$

$Th8$：$\vdash_{PC}A\rightarrow(\neg A\rightarrow B)$

1. $\neg A\rightarrow (A\rightarrow B)$,$Th7$
2. $A\rightarrow(\neg A\rightarrow B)$,$Th2$

$Th9$：$\vdash_{PC}(\neg A\rightarrow A)\rightarrow A$

1. $\neg A\rightarrow(A\rightarrow\neg(\neg A\rightarrow A))$,$Th7$
2. $(\neg A\rightarrow(A\rightarrow\neg(\neg A\rightarrow A)))\rightarrow((\neg A\rightarrow A)\rightarrow(\neg A\rightarrow\neg(\neg A\rightarrow A)))$,$A2$
3. $(\neg A\rightarrow A)\rightarrow(\neg A\rightarrow\neg(\neg A\rightarrow A))$,$r_{mp}(1)(2)$
4. $(\neg A\rightarrow\neg(\neg A\rightarrow A))\rightarrow((\neg A\rightarrow A)\rightarrow A)$,$A3$
5. $(\neg A\rightarrow A)\rightarrow((\neg A\rightarrow A)\rightarrow A)$,$Th6$
6. $((\neg A\rightarrow A)\rightarrow((\neg A\rightarrow A)\rightarrow A))\rightarrow(((\neg A\rightarrow A)\rightarrow(\neg A\rightarrow A))\rightarrow((\neg A\rightarrow A)\rightarrow A))$,$A2$
7. $((\neg A\rightarrow A)\rightarrow(\neg A\rightarrow A))\rightarrow((\neg A\rightarrow A)\rightarrow A)$,$r_{mp}(5)(6)$
8. $(\neg A\rightarrow A)\rightarrow(\neg A\rightarrow A)$,$Th1$
9. $(\neg A\rightarrow A)\rightarrow A$,$r_{mp}(7)(8)$

$Th10$：$\vdash_{PC}\neg\neg A\rightarrow A$

1. $\neg\neg A\rightarrow(\neg A\rightarrow\neg\neg\neg A)$,$Th7$
2. $(\neg A\rightarrow\neg\neg\neg A)\rightarrow(\neg\neg A\rightarrow A)$,$A3$
3. $\neg\neg A\rightarrow(\neg\neg A\rightarrow A)$,$Th6$
4. $(\neg\neg A\rightarrow(\neg\neg A\rightarrow A))\rightarrow((\neg\neg A\rightarrow\neg\neg A)\rightarrow(\neg\neg A\rightarrow A))$,$A2$
5. $(\neg\neg A\rightarrow\neg\neg A)\rightarrow(\neg\neg A\rightarrow A)$,$r_{mp}(3)(4)$
6. $\neg\neg A\rightarrow\neg\neg A$,$Th1$
7. $\neg\neg A\rightarrow A$,$r_{mp}(5)(6)$

$Th11$：$\vdash_{PC}(A\rightarrow\neg A)\rightarrow\neg A$

1. $\neg\neg A\rightarrow A$,$Th10$
2. $(\neg\neg A\rightarrow A)\rightarrow((A\rightarrow\neg A)\rightarrow(\neg\neg A\rightarrow\neg A))$,$Th5$
3. $(A\rightarrow\neg A)\rightarrow(\neg\neg A\rightarrow\neg A)$,$r_{mp}(1)(2)$
4. $(\neg\neg A\rightarrow\neg A)\rightarrow\neg A$,$Th9$
5. $(A\rightarrow\neg A)\rightarrow\neg A$,$Th6$

$Th12$：$\vdash_{PC}A\rightarrow\neg\neg A$

1. $A\rightarrow(\neg A\rightarrow\neg\neg A)$,$Th8$
2. $(\neg A\rightarrow\neg\neg A)\rightarrow\neg\neg A$,$Th11$
3. $A\rightarrow\neg\neg A$,$r_{mp}(1)(2)$

$Th13$：$\vdash_{PC}(A\rightarrow B)\rightarrow(\neg B\rightarrow\neg A)$

1. $(\neg\neg A\rightarrow\neg\neg B)\rightarrow(\neg B\rightarrow\neg A)$,$A3$
2. $B\rightarrow\neg\neg B$,$Th12$
3. $(B\rightarrow\neg\neg B)\rightarrow((\neg\neg A\rightarrow B)\rightarrow(\neg\neg A\rightarrow\neg\neg B))$,$A2$
4. $(\neg\neg A\rightarrow B)\rightarrow(\neg\neg A\rightarrow\neg\neg B)$,$r_{mp}(2)(3)$
5. $(\neg\neg A\rightarrow B)\rightarrow(\neg B\rightarrow\neg A)$,$Th6$
6. $\neg\neg A\rightarrow A$,$Th10$
7. $(\neg\neg A\rightarrow A)\rightarrow((A\rightarrow B)\rightarrow(\neg\neg A\rightarrow B))$,$Th5$
8. $(A\rightarrow B)\rightarrow(\neg\neg A\rightarrow B)$,$r_{mp}(6)(7)$
9. $(A\rightarrow B)\rightarrow(\neg B\rightarrow\neg A)$,$Th6$

$Th14$：$\vdash_{PC}(\neg A\rightarrow B)\rightarrow(\neg B\rightarrow A)$

1. $(\neg A\rightarrow\neg\neg B)\rightarrow(\neg B\rightarrow A)$,$A3$
2. $B\rightarrow\neg\neg B$,$Th12$
3. $(B\rightarrow\neg\neg B)\rightarrow((\neg A\rightarrow B)\rightarrow(\neg A\rightarrow\neg\neg B))$,$Th4$
4. $(\neg A\rightarrow B)\rightarrow(\neg A\rightarrow\neg\neg B)$,$r_{mp}(2)(3)$
5. $(\neg A\rightarrow B)\rightarrow(\neg B\rightarrow A)$,$Th6$

$Th15$：$\vdash_{PC}(A\rightarrow\neg B)\rightarrow(B\rightarrow\neg A)$

1. $(\neg\neg A\rightarrow\neg B)\rightarrow(B\rightarrow\neg A)$,$A3$
2. $\neg\neg A\rightarrow A$,$Th10$
3. $(\neg\neg A\rightarrow A)\rightarrow((A\rightarrow\neg B)\rightarrow(\neg\neg A\rightarrow\neg B))$,$Th5$
4. $(A\rightarrow\neg B)\rightarrow(\neg\neg A\rightarrow\neg B)$,$r_{mp}(2)(3)$
5. $(A\rightarrow\neg B)\rightarrow(B\rightarrow\neg A)$,$Th6$

反证法

$Th16$：$\vdash_{PC}(\neg A\rightarrow B)\rightarrow((\neg A\rightarrow\neg B)\rightarrow A)$

1. $(\neg A\rightarrow\neg B)\rightarrow(B\rightarrow A)$,$A3$
2. $B\rightarrow((\neg A\rightarrow\neg B)\rightarrow A)$,$Th2$
3. $((\neg A\rightarrow\neg B)\rightarrow A)\rightarrow(\neg A\rightarrow\neg(\neg A\rightarrow\neg B))$,$Th13$
4. $B\rightarrow(\neg A\rightarrow\neg(\neg A\rightarrow\neg B))$,$r_{mp}(2)(3)$
5. $\neg A\rightarrow(B\rightarrow\neg(\neg A\rightarrow\neg B))$,$Th2$
6. $(\neg A\rightarrow(B\rightarrow\neg(\neg A\rightarrow\neg B)))\rightarrow((\neg A\rightarrow B)\rightarrow(\neg A\rightarrow\neg(\neg A\rightarrow\neg B)))$,$A2$
7. $(\neg A\rightarrow B)\rightarrow(\neg A\rightarrow\neg(\neg A\rightarrow\neg B))$,$r_{mp}(5)(6)$
8. $(\neg A\rightarrow\neg(\neg A\rightarrow\neg B))\rightarrow((\neg A\rightarrow\neg B)\rightarrow A)$,$A3$
9. $(\neg A\rightarrow B)\rightarrow((\neg A\rightarrow\neg B)\rightarrow A)$,$Th6$

$Th17$：$\vdash_{PC}(A\rightarrow B)\rightarrow((A\rightarrow\neg B)\rightarrow\neg A)$

1. $(A\rightarrow\neg B)\rightarrow((A\rightarrow\neg B)\rightarrow\neg A)$,$Th15$
2. $B\rightarrow((A\rightarrow\neg B)\rightarrow\neg A)$,$Th3$
3. $((A\rightarrow\neg B)\rightarrow\neg A)\rightarrow(A\rightarrow\neg(A\rightarrow\neg B))$,$Th15$
4. $B\rightarrow(A\rightarrow\neg(A\rightarrow\neg B))$,$Th6$
5. $A\rightarrow(B\rightarrow\neg(A\rightarrow\neg B))$,$Th2$
6. $(A\rightarrow(B\rightarrow\neg(A\rightarrow\neg B)))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow\neg(A\rightarrow\neg B)))$,$A2$
7. $(A\rightarrow B)\rightarrow(A\rightarrow\neg(A\rightarrow\neg B))$,$r_{mp}(5)(6)$
8. $(A\rightarrow\neg(A\rightarrow\neg B))\rightarrow((A\rightarrow\neg B)\rightarrow\neg A)$,$Th15$
9. $(A\rightarrow B)\rightarrow((A\rightarrow\neg B)\rightarrow\neg A)$,$Th6$

→拆分

$Th18$：$\vdash_{PC}\neg A\rightarrow C,\vdash_{PC}B\rightarrow C$当且仅当$\vdash_{PC}(A\rightarrow B)\rightarrow C$

当$\vdash_{PC}(A\rightarrow B)\rightarrow C$时：

1. $(A\rightarrow B)\rightarrow C$
2. $B\rightarrow(A\rightarrow B)$,$A1$
3. $B\rightarrow C$,$Th6$
4. $\neg A\rightarrow(A\rightarrow B)$,$Th7$
5. $\neg A\rightarrow C$,$Th6$

当$\vdash_{PC}\neg A\rightarrow C,\vdash_{PC}B\rightarrow C$时：

1. $\neg A\rightarrow C$
2. $B\rightarrow C$
3. $(B\rightarrow C)\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$,$Th4$
4. $(A\rightarrow B)\rightarrow(A\rightarrow C)$,$r_{mp}(2)(3)$
5. $(\neg A\rightarrow C)\rightarrow(\neg C\rightarrow A)$,$Th14$
6. $\neg C\rightarrow A$,$r_{mp}(1)(5)$
7. $(\neg C\rightarrow A)\rightarrow((A\rightarrow C)\rightarrow(\neg C\rightarrow C))$,$Th5$
8. $(A\rightarrow C)\rightarrow(\neg C\rightarrow C)$,$r_{mp}(6)(7)$
9. $(A\rightarrow B)\rightarrow(\neg C\rightarrow C)$,$Th2$
10. $(\neg C\rightarrow C)\rightarrow C$,$Th9$
11. $(A\rightarrow B)\rightarrow C$,$Th6$

$Th19$：定义$A\vee B =_ {df}\neg A\rightarrow B$，$\vdash_{PC}A\rightarrow A\vee B$

1. $A\rightarrow(\neg A\rightarrow B)$,$Th8$

$Th20$：$\vdash_{PC}A\rightarrow B\vee A$

1. $A\rightarrow(\neg B\rightarrow A)$,$A1$

$Th21$：如果$\vdash_{PC}P\rightarrow Q,\vdash_{PC}R\rightarrow S$，那么$\vdash_{PC}(Q\rightarrow R)\rightarrow(P\rightarrow S)$

1. $P\rightarrow Q$
2. $(P\rightarrow Q)\rightarrow((Q\rightarrow R)\rightarrow(P\rightarrow R))$,$Th5$
3. $(Q\rightarrow R)\rightarrow(P\rightarrow R)$,$r_{mp}(1)(2)$
4. $R\rightarrow S$
5. $(R\rightarrow S)\rightarrow((P\rightarrow R)\rightarrow(P\rightarrow S))$,$Th4$
6. $(P\rightarrow R)\rightarrow(P\rightarrow S)$,$r_{mp}(4)(5)$
7. $(Q\rightarrow R)\rightarrow(P\rightarrow S)$,$Th6$

$Th22$：$\vdash_{PC}(A\rightarrow C)\rightarrow((B\rightarrow C)\rightarrow((A\vee B)\rightarrow C))$

1. $(\neg A\rightarrow B)\rightarrow(\neg A\rightarrow B)$,$Th1$
2. $\neg A\rightarrow((\neg A\rightarrow B)\rightarrow B)$,$Th2$
3. $((\neg A\rightarrow B)\rightarrow B)\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B))$,$Th13$
4. $\neg A\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B))$,$Th6$
5. $(\neg A\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B)))\rightarrow(\neg C\rightarrow(\neg A\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B))))$,$A1$
6. $\neg C\rightarrow(\neg A\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B)))$,$r_{mp}(4)(5)$
7. $(\neg C\rightarrow(\neg A\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B))))\rightarrow((\neg C\rightarrow\neg A)\rightarrow(\neg C\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B))))$,$A2$
8. $(\neg C\rightarrow\neg A)\rightarrow(\neg C\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B)))$,$r_{mp}(6)(7)$
9. $(\neg C\rightarrow(\neg B\rightarrow\neg(\neg A\rightarrow B)))\rightarrow((\neg C\rightarrow\neg B)\rightarrow(\neg C\rightarrow\neg(\neg A\rightarrow B)))$,$A2$
10. $(\neg C\rightarrow\neg A)\rightarrow((\neg C\rightarrow\neg B)\rightarrow(\neg C\rightarrow\neg(\neg A\rightarrow B)))$,$Th6$
11. $(A\rightarrow C)\rightarrow(\neg C\rightarrow\neg A)$,$Th13$
12. $(A\rightarrow C)\rightarrow((\neg C\rightarrow\neg B)\rightarrow(\neg C\rightarrow\neg(\neg A\rightarrow B)))$,$Th6$
13. $(B\rightarrow C)\rightarrow(\neg C\rightarrow\neg B)$,$Th13$
14. $(\neg C\rightarrow\neg(\neg A\rightarrow B))\rightarrow((\neg A\rightarrow B)\rightarrow C)$,$A3$
15. $((\neg C\rightarrow(\neg C\rightarrow\neg(\neg A\rightarrow B)))\rightarrow(\neg C\rightarrow\neg B))\rightarrow((B\rightarrow C)\rightarrow((\neg A\rightarrow B)\rightarrow C))$,$Th21$
16. $(A\rightarrow C)\rightarrow((B\rightarrow C)\rightarrow((\neg A\rightarrow B)\rightarrow C))$,$Th6$

$Th23$： 定义$A\wedge B =_ {df} \neg(A\rightarrow\neg B)$，那么$\vdash_{PC}A\wedge B\rightarrow C$当且仅当$\vdash_{PC}A\rightarrow(B\rightarrow C)$

当$\vdash_{PC}A\wedge B\rightarrow C$时：

1. $\neg(A\rightarrow\neg B)\rightarrow C$
2. $(\neg(A\rightarrow\neg B)\rightarrow C)\rightarrow(\neg C\rightarrow(A\rightarrow\neg B))$,$Th14$
3. $\neg C\rightarrow(A\rightarrow\neg B)$,$r_{mp}(1)(2)$
4. $A\rightarrow(\neg C\rightarrow\neg B)$,$Th2$
5. $(\neg C\rightarrow\neg B)\rightarrow(B\rightarrow C)$,$A3$
6. $A\rightarrow(B\rightarrow C)$,$Th6$

当$\vdash_{PC}A\rightarrow(B\rightarrow C)$时：

1. $A\rightarrow(B\rightarrow C)$
2. $(B\rightarrow C)\rightarrow(\neg C\rightarrow\neg B)$,$Th13$
3. $A\rightarrow(\neg C\rightarrow\neg B)$,$Th6$
4. $\neg C\rightarrow(A\rightarrow\neg B)$,$Th2$
5. $(\neg C\rightarrow(A\rightarrow\neg B))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow C)$,$Th14$
6. $\neg(A\rightarrow\neg B)\rightarrow C$,$r_{mp}(4)(5)$

$Th24$：$\vdash_{PC}A\wedge B\rightarrow A$

1. $\neg A\rightarrow(A\rightarrow\neg B)$,$Th7$
2. $(\neg A\rightarrow(A\rightarrow\neg B))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow A)$,$Th14$
3. $\neg(A\rightarrow\neg B)\rightarrow A$,$r_{mp}(1)(2)$

$Th25$：$\vdash_{PC}B\wedge A\rightarrow A$

1. $\neg B\rightarrow(A\rightarrow\neg B)$,$A1$
2. $(\neg B\rightarrow(A\rightarrow\neg B))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow B)$,$Th14$
3. $\neg(A\rightarrow\neg B)\rightarrow B$,$r_{mp}(1)(2)$

$Th26$：$\vdash_{PC}A\rightarrow(B\rightarrow A\wedge B)$

1. $A\wedge B\rightarrow A\wedge B$,$Th1$
2. $A\rightarrow(B\rightarrow A\wedge B)$,$Th23$

$Th27$：$\vdash_{PC}(A\rightarrow B)\rightarrow((A\rightarrow C)\rightarrow(A\rightarrow B\wedge C))$

1. $B\rightarrow(C\rightarrow B\wedge C)$,$Th26$
2. $(B\rightarrow(C\rightarrow B\wedge C))\rightarrow(A\rightarrow(B\rightarrow(C\rightarrow B\wedge C)))$,$A1$
3. $A\rightarrow(B\rightarrow(C\rightarrow B\wedge C))$,$r_{mp}(1)(2)$
4. $(A\rightarrow(B\rightarrow(C\rightarrow B\wedge C)))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow(C\rightarrow B\wedge C)))$,$A2$
5. $(A\rightarrow B)\rightarrow(A\rightarrow(C\rightarrow B\wedge C))$,$r_{mp}(3)(4)$
6. $A\rightarrow((A\rightarrow B)\rightarrow(C\rightarrow B\wedge C))$,$Th2$
7. $((A\rightarrow B)\rightarrow(C\rightarrow B\wedge C))\rightarrow((A\rightarrow C)\rightarrow(A\rightarrow B\wedge C))$,$A2$
8. $A\rightarrow((A\rightarrow C)\rightarrow(A\rightarrow B\wedge C))$,$Th6$

$Th28$：我们将$\vdash_{PC}P\rightarrow Q,\vdash_{PC}Q\rightarrow P$记作$\vdash_{PC}P\leftrightarrow Q$，那么有$\vdash_{PC}A\vee B\leftrightarrow B\vee A$

1. $(\neg A\rightarrow B)\rightarrow(\neg B\rightarrow A)$,$Th14$
2. $(\neg B\rightarrow A)\rightarrow(\neg A\rightarrow B)$,$Th14$

$Th29$：$\vdash_{PC}A\wedge B\leftrightarrow B\wedge A$

1. $(A\rightarrow\neg B)\rightarrow(B\rightarrow\neg A)$,$Th15$
2. $(B\rightarrow\neg A)\rightarrow(A\rightarrow\neg B)$,$Th15$

$Th30$：$\vdash_{PC}(A\vee B)\vee C\leftrightarrow A\vee(B\vee C)$

1. $B\rightarrow(\neg B\rightarrow C)$,$Th8$
2. $(B\rightarrow(\neg B\rightarrow C))\rightarrow((\neg A\rightarrow B)\rightarrow(\neg A\rightarrow(\neg B\rightarrow C)))$,$A2$
3. $(\neg A\rightarrow B)\rightarrow(\neg A\rightarrow(\neg B\rightarrow C))$,$r_{mp}(1)(2)$
4. $\neg\neg(\neg A\rightarrow B)\rightarrow(\neg A\rightarrow B)$,$Th10$
5. $\neg\neg(\neg A\rightarrow B)\rightarrow(\neg A\rightarrow(\neg B\rightarrow C))$,$Th6$
6. $C\rightarrow(\neg B\rightarrow C)$,$A1$
7. $(C\rightarrow(\neg B\rightarrow C))\rightarrow(\neg A\rightarrow(C\rightarrow(\neg B\rightarrow C)))$,$A1$
8. $\neg A\rightarrow(C\rightarrow(\neg B\rightarrow C))$,$r_{mp}(6)(7)$
9. $C\rightarrow(\neg A\rightarrow(\neg B\rightarrow C))$,$Th2$
10. $(\neg(\neg A\rightarrow B)\rightarrow C)\rightarrow(\neg A\rightarrow(\neg B\rightarrow C))$,$Th18$
11. $B\rightarrow(\neg A\rightarrow B)$,$A1$
12. $(B\rightarrow(\neg A\rightarrow B))\rightarrow(\neg(\neg A\rightarrow B)\rightarrow\neg B)$,$Th13$
13. $\neg(\neg A\rightarrow B)\rightarrow\neg B$,$r_{mp}(11)(12)$
14. $(\neg(\neg A\rightarrow B)\rightarrow\neg B)\rightarrow((\neg B\rightarrow C)\rightarrow(\neg(\neg A\rightarrow B)\rightarrow C))$,$Th5$
15. $(\neg B\rightarrow C)\rightarrow(\neg(\neg A\rightarrow B)\rightarrow C)$,$r_{mp}(13)(14)$
16. $\neg A\rightarrow(A\rightarrow C)$,$Th7$
17. $A\rightarrow(\neg A\rightarrow B)$,$Th8$
18. $(A\rightarrow(\neg A\rightarrow B))\rightarrow(\neg(\neg A\rightarrow B)\rightarrow\neg A)$,$Th13$
19. $\neg(\neg A\rightarrow B)\rightarrow\neg A$,$r_{mp}(17)(18)$
20. $(\neg(\neg A\rightarrow B)\rightarrow\neg A)\rightarrow(A\rightarrow(\neg(\neg A\rightarrow B)\rightarrow\neg A))$,$A1$
21. $A\rightarrow(\neg(\neg A\rightarrow B)\rightarrow\neg A)$,$r_{mp}(19)(20)$
22. $\neg\neg A\rightarrow A$,$Th10$
23. $\neg\neg A\rightarrow(\neg(\neg A\rightarrow B)\rightarrow\neg A)$,$Th6$
24. $(\neg A\rightarrow(\neg B\rightarrow C))\rightarrow(\neg(\neg A\rightarrow B)\rightarrow C)$,$Th18$

$Th31$：$\vdash_{PC}(A\wedge B)\wedge C\leftrightarrow A\wedge(B\wedge C)$

1. $(B\rightarrow\neg C)\rightarrow(C\rightarrow\neg B)$,$Th15$
2. $((B\rightarrow\neg C)\rightarrow(C\rightarrow\neg B))\rightarrow((A\rightarrow(B\rightarrow\neg C))\rightarrow(A\rightarrow(C\rightarrow\neg B)))$,$Th4$
3. $(A\rightarrow(B\rightarrow\neg C))\rightarrow(A\rightarrow(C\rightarrow\neg B))$,$r_{mp}(1)(2)$
4. $(A\rightarrow(C\rightarrow\neg B))\rightarrow(C\rightarrow(A\rightarrow\neg B))$,$Th3$
5. $(A\rightarrow(B\rightarrow\neg C))\rightarrow(C\rightarrow(A\rightarrow\neg B))$,$Th6$
6. $\neg\neg(B\rightarrow\neg C)\rightarrow(B\rightarrow\neg C)$,$Th10$
7. $(\neg\neg(B\rightarrow\neg C)\rightarrow(B\rightarrow\neg C))\rightarrow((A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow(A\rightarrow(B\rightarrow\neg C)))$,$Th4$
8. $(A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow(A\rightarrow(B\rightarrow\neg C))$,$r_{mp}(6)(7)$
9. $(A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow(C\rightarrow(A\rightarrow\neg B))$,$Th6$
10. $(C\rightarrow(A\rightarrow\neg B))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow\neg C)$,$Th13$
11. $(A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow\neg C)$,$Th6$
12. $((A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow\neg C))\rightarrow(\neg(\neg(A\rightarrow\neg B)\rightarrow\neg C)\rightarrow\neg(A\rightarrow\neg\neg(B\rightarrow\neg C)))$,$Th13$
13. $\neg(\neg(A\rightarrow\neg B)\rightarrow\neg C)\rightarrow\neg(A\rightarrow\neg\neg(B\rightarrow\neg C))$,$r_{mp}(11)(12)$
14. $(C\rightarrow\neg B)\rightarrow(B\rightarrow\neg C)$,$Th15$
15. $((C\rightarrow\neg B)\rightarrow(B\rightarrow\neg C))\rightarrow((A\rightarrow(C\rightarrow\neg B))\rightarrow(A\rightarrow(B\rightarrow\neg C)))$,$Th4$
16. $(A\rightarrow(C\rightarrow\neg B))\rightarrow(A\rightarrow(B\rightarrow\neg C))$,$r_{mp}(14)(15)$
17. $(C\rightarrow(A\rightarrow\neg B))\rightarrow(A\rightarrow(C\rightarrow\neg B))$,$Th3$
18. $(C\rightarrow(A\rightarrow\neg B))\rightarrow(A\rightarrow(B\rightarrow\neg C))$,$Th6$
19. $(B\rightarrow\neg C)\rightarrow\neg\neg(B\rightarrow\neg C)$,$Th12$
20. $((B\rightarrow\neg C)\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow((A\rightarrow(B\rightarrow\neg C))\rightarrow(A\rightarrow\neg\neg(B\rightarrow\neg C)))$,$Th4$
21. $(A\rightarrow(B\rightarrow\neg C))\rightarrow(A\rightarrow\neg\neg(B\rightarrow\neg C))$,$r_{mp}(19)(20)$
22. $(C\rightarrow(A\rightarrow\neg B))\rightarrow(A\rightarrow\neg\neg(B\rightarrow\neg C))$,$Th6$
23. $(\neg(A\rightarrow\neg B)\rightarrow\neg C)\rightarrow(C\rightarrow(A\rightarrow\neg B))$,$A3$
24. $(\neg(A\rightarrow\neg B)\rightarrow\neg C)\rightarrow(A\rightarrow\neg\neg(B\rightarrow\neg C))$,$Th6$
25. $((\neg(A\rightarrow\neg B)\rightarrow\neg C)\rightarrow(A\rightarrow\neg\neg(B\rightarrow\neg C)))\rightarrow(\neg(A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow\neg(\neg(A\rightarrow\neg B)\rightarrow\neg C))$,$Th13$
26. $\neg(A\rightarrow\neg\neg(B\rightarrow\neg C))\rightarrow\neg(\neg(A\rightarrow\neg B)\rightarrow\neg C)$,$r_{mp}(24)(25)$

$Th32$：$\vdash_{PC}A\wedge(A\vee B)\leftrightarrow A$

1. $A\rightarrow(A\vee B\rightarrow A)$,$A1$
2. $A\wedge(A \vee B)\rightarrow A$,$Th23$
3. $\neg A\rightarrow\neg A$,$Th1$
4. $A\rightarrow(\neg A\rightarrow B)$,$Th8$
5. $(A\rightarrow(\neg A\rightarrow B))\rightarrow(\neg(\neg A\rightarrow B)\rightarrow\neg A)$,$Th13$
6. $\neg(\neg A\rightarrow B)\rightarrow\neg A$,$r_{mp}(4)(5)$
7. $((\neg A\rightarrow B)\rightarrow\neg A)\rightarrow\neg A$,$Th18$
8. $(A\rightarrow\neg(\neg A\rightarrow B))\rightarrow((\neg A\rightarrow B)\rightarrow\neg A)$,$Th15$
9. $(A\rightarrow\neg(\neg A\rightarrow B))\rightarrow\neg A$,$Th6$
10. $((A\rightarrow\neg(\neg A\rightarrow B))\rightarrow\neg A)\rightarrow(A\rightarrow\neg(A\rightarrow\neg(\neg A\rightarrow B)))$,$Th15$
11. $A\rightarrow\neg(A\rightarrow\neg(\neg A\rightarrow B))$,$r_{mp}(9)(10)$

$Th33$：$\vdash_{PC}A\vee(A\wedge B)\leftrightarrow A$

1. $A\rightarrow(\neg A\rightarrow(A\wedge B))$,$Th8$
2. $A\wedge B\rightarrow A$,$Th24$
3. $(A\wedge B\rightarrow A)\rightarrow((\neg A\rightarrow(A\wedge B))\rightarrow(\neg A\rightarrow A))$,$Th4$
4. $(\neg A\rightarrow(A\wedge B))\rightarrow(\neg A\rightarrow A)$,$r_{mp}(2)(3)$
5. $(\neg A\rightarrow A)\rightarrow A$,$Th9$
6. $(\neg A\rightarrow(A\wedge B))\rightarrow A$,$Th6$

$Th34$：$\vdash_{PC}A\wedge(B\vee C)\leftrightarrow(A\wedge B)\vee(A\wedge C)$

1. $B\rightarrow(\neg B\rightarrow C)$,$Th8$
2. $(B\rightarrow(\neg B\rightarrow C))\rightarrow(\neg(\neg B\rightarrow C)\rightarrow\neg B)$,$Th13$
3. $\neg(\neg B\rightarrow C)\rightarrow\neg B$,$r_{mp}(1)(2)$
4. $(\neg(\neg B\rightarrow C)\rightarrow\neg B)\rightarrow((A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(A\rightarrow\neg B))$,$Th4$
5. $(A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(A\rightarrow\neg B)$,$r_{mp}(3)(4)$
6. $((A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(A\rightarrow\neg B))\rightarrow(\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg(\neg B\rightarrow C)))$,$Th13$
7. $\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg(\neg B\rightarrow C))$,$r_{mp}(5)(6)$
8. $C\rightarrow(\neg B\rightarrow C)$,$A1$
9. $(C\rightarrow(\neg B\rightarrow C))\rightarrow(\neg(\neg B\rightarrow C)\rightarrow\neg C)$,$Th13$
10. $\neg(\neg B\rightarrow C)\rightarrow\neg C$,$r_{mp}(8)(9)$
11. $(\neg(\neg B\rightarrow C)\rightarrow\neg C)\rightarrow((A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(A\rightarrow\neg C))$,$Th4$
12. $(A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(A\rightarrow\neg C)$,$r_{mp}(10)(11)$
13. $((A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(A\rightarrow\neg C))\rightarrow(\neg(A\rightarrow\neg C)\rightarrow\neg(A\rightarrow\neg(\neg B\rightarrow C)))$,$Th13$
14. $\neg(A\rightarrow\neg C)\rightarrow\neg(A\rightarrow\neg(\neg B\rightarrow C))$,$r_{mp}(12)(13)$
15. $((A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))\rightarrow\neg(A\rightarrow\neg(\neg B\rightarrow C))$,$Th18$
16. $(A\rightarrow\neg B)\rightarrow\neg\neg(A\rightarrow\neg B)$,$Th12$
17. $((A\rightarrow\neg B)\rightarrow\neg\neg(A\rightarrow\neg B))\rightarrow((\neg\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))\rightarrow((A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C)))$,$Th5$
18. $(\neg\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))\rightarrow((A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))$,$r_{mp}(16)(17)$
19. $(\neg\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))\rightarrow\neg(A\rightarrow\neg(\neg B\rightarrow C))$,$Th6$
20. $(A\rightarrow\neg B)\rightarrow((A\rightarrow\neg C)\rightarrow(A\rightarrow\neg(\neg B\rightarrow C)))$,$Th23$
21. $((A\rightarrow\neg C)\rightarrow(A\rightarrow\neg(\neg B\rightarrow C)))\rightarrow(\neg(A\rightarrow\neg(\neg B\rightarrow C))\rightarrow\neg(A\rightarrow\neg C))$,$Th13$
22. $(A\rightarrow\neg B)\rightarrow(\neg(A\rightarrow\neg(\neg B\rightarrow C))\rightarrow\neg(A\rightarrow\neg C))$,$Th6$
23. $\neg(A\rightarrow\neg(\neg B\rightarrow C))\rightarrow((A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))$,$Th2$
24. $\neg\neg(A\rightarrow\neg B)\rightarrow(A\rightarrow\neg B)$,$Th10$
25. $(\neg\neg(A\rightarrow\neg B)\rightarrow(A\rightarrow\neg B))\rightarrow(((A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))\rightarrow(\neg\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C)))$,$Th5$
26. $((A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))\rightarrow(\neg\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))$,$r_{mp}(24)(25)$
27. $\neg(A\rightarrow\neg(\neg B\rightarrow C))\rightarrow(\neg\neg(A\rightarrow\neg B)\rightarrow\neg(A\rightarrow\neg C))$,$Th6$

$Th35$：$\vdash_{PC}A\vee(B\wedge C)\leftrightarrow(A\vee B)\wedge(A\vee C)$

1. $B\wedge C\rightarrow B$,$Th24$
2. $(B\wedge C\rightarrow B)\rightarrow((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow B))$,$Th4$
3. $(\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow B)$,$r_{mp}(1)(2)$
4. $((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow B))\rightarrow(((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow C))\rightarrow((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow B)\wedge(\neg A\rightarrow C)))$
5. $((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow C))\rightarrow((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow B)\wedge(\neg A\rightarrow C))$,$r_{mp}(3)(4)$
6. $B\wedge C\rightarrow C$,$Th25$
7. $(B\wedge C\rightarrow C)\rightarrow((\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow C))$,$Th4$
8. $(\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow C)$,$r_{mp}(6)(7)$
9. $(\neg A\rightarrow(B\wedge C))\rightarrow(\neg A\rightarrow B)\wedge(\neg A\rightarrow C)$,$r_{mp}(5)(8)$
10. $(\neg A\rightarrow B)\rightarrow((\neg A\rightarrow C)\rightarrow(\neg A\rightarrow B\wedge C))$,$Th27$
11. $(\neg A\rightarrow B)\wedge(\neg A\rightarrow C)\rightarrow(\neg A\rightarrow B\wedge C)$,$Th23$

上述的35个PC的定理都是十分重要和有用的，其中定理$Th16$（反证法）和$Th18$（→拆分法）可以帮助我们将定理更加系统地证明，下面我们举两个例子进行说明。

PC的基本定理的运用

运用$Th16$证明：$\vdash_{PC}((A\rightarrow B)\rightarrow A)\rightarrow A$

如果我们要运用$Th16$，我们就需要假设这个定理不成立从而推出矛盾，不妨证明：

$\vdash_{PC}\neg(((A\rightarrow B)\rightarrow A)\rightarrow A)\rightarrow(A\rightarrow B)$

$\vdash_{PC}\neg(((A\rightarrow B)\rightarrow A)\rightarrow A)\rightarrow\neg(A\rightarrow B)$

后者即证：$\vdash_{PC}((A\rightarrow B)\rightarrow A)\rightarrow((A\rightarrow B)\rightarrow A)$，结论是显然的。

前者即证：$\vdash_{PC}((A\rightarrow B)\rightarrow A)\rightarrow(\neg(A\rightarrow B)\rightarrow A)$

后件可以由$\neg A\rightarrow(A\rightarrow B)$变形得到，所以得证。

运用$Th18$证明：$\vdash_{PC}(A\rightarrow C)\rightarrow((B\rightarrow C)\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

运用$Th18$证明这个定理等价于证明：

$\vdash_{PC}\neg A\rightarrow((B\rightarrow C)\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

$\vdash_{PC}C\rightarrow((B\rightarrow C)\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

后者即证：$\vdash_{PC}(B\rightarrow C)\rightarrow(C\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

其后件是$A1$，故结论是显然的。

现在我们只需要证明：$\vdash_{PC}\neg A\rightarrow((B\rightarrow C)\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

即证：$\vdash_{PC}(B\rightarrow C)\rightarrow(\neg A\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

再次运用$Th18$，即证：

$\vdash_{PC}\neg B\rightarrow(\neg A\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

$\vdash_{PC}C\rightarrow(\neg A\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

后者即证$\vdash_{PC}\neg A\rightarrow(C\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

其后件是$A1$，故结论是显然的。

现在我们只需要证明：$\vdash_{PC}\neg B\rightarrow(\neg A\rightarrow(((A\rightarrow B)\rightarrow B)\rightarrow C))$

即证：$\vdash_{PC}((A\rightarrow B)\rightarrow B)\rightarrow(\neg B\rightarrow(\neg A\rightarrow C))$

再次运用$Th18$，即证：

$\vdash_{PC}\neg(A\rightarrow B)\rightarrow(\neg B\rightarrow(\neg A\rightarrow C))$

$\vdash_{PC}B\rightarrow(\neg B\rightarrow(\neg A\rightarrow C))$

后者是$Th8$，故结论是显然的。

现在我们只需要证明：$\vdash_{PC}\neg(A\rightarrow B)\rightarrow(\neg B\rightarrow(\neg A\rightarrow C))$

即证：$\vdash_{PC}\neg B\rightarrow(\neg A\rightarrow(\neg C\rightarrow (A\rightarrow B)))$

不妨证：$\vdash_{PC}\neg A\rightarrow(\neg C\rightarrow (A\rightarrow B))$

可知有：

$\vdash_{PC}\neg A\rightarrow(A\rightarrow B)$

$\vdash_{PC}(A\rightarrow B)\rightarrow(\neg C\rightarrow(A\rightarrow B))$

按照上述思路将对应的证明序列写出即可证明该定理。

演绎定理

证明：$\vdash_{PC}(A\rightarrow(B\rightarrow C))\rightarrow((C\rightarrow D)\rightarrow(A\rightarrow(B\rightarrow D)))$

1. $(C\rightarrow D)\rightarrow((B\rightarrow C)\rightarrow(B\rightarrow D))$,$Th4$
2. $((B\rightarrow C)\rightarrow(B\rightarrow D))\rightarrow((A\rightarrow(B\rightarrow C))\rightarrow(A\rightarrow(B\rightarrow D)))$,$Th4$
3. $(C\rightarrow D)\rightarrow((A\rightarrow(B\rightarrow C))\rightarrow(A\rightarrow(B\rightarrow D)))$,$Th6$
4. $(A\rightarrow(B\rightarrow C))\rightarrow((C\rightarrow D)\rightarrow(A\rightarrow(B\rightarrow D)))$,$Th2$

上面这个例子表明，在PC中证明定理的这个过程中的公式序列的公式长度通常较长，为了缩短公式序列的长度，我们现在给出PC中一个重要方便的定理：演绎定理。

演绎定理：对PC中任意公式集合$\Gamma$和公式$A,B$，$\Gamma\cup${$A$}$\vdash_{PC}B$（或记为$\Gamma;A\vdash_{PC}B$）当且仅当$\Gamma\vdash_{PC}A\rightarrow B$。

证明：（充分性）

已知$\Gamma\vdash_{PC}A\rightarrow B$

从$\Gamma$出发在PC可以得到一个$A\rightarrow B$的演绎序列$A_1,A_2,\cdots,A_n(=A\rightarrow B)$

从$\Gamma\cup${$A$}出发在PC也可以得到一个$A\rightarrow B$的演绎序列$A_1,A_2,\cdots,A_n(=A\rightarrow B)$

从$\Gamma\cup${$A$}出发在PC中可以得到$B$的一个演绎序列$A_1,A_2,\cdots,A_n(=A\rightarrow B),A,B$

也就是说有$\Gamma;A\vdash_{PC}B$。 证明：（必要性）

已知$\Gamma\cup${$A$}$\vdash_{PC}B$

从$\Gamma\cup${$A$}出发在PC可以得到一个$B$的演绎序列$B_1,B_2,\cdots,B_k(=B)$，我们对演绎序列的长度$k$使用数学归纳法：

当$k=1$时可知$B$或是公理、或有$B\in\Gamma\cup${$A$}：

当$B$是公理时，$A\rightarrow B$有演绎序列$B,B\rightarrow(A\rightarrow B),A\rightarrow B$。

当$B\in\Gamma$时，$A\rightarrow B$有演绎序列$B,B\rightarrow(A\rightarrow B),A\rightarrow B$。

当$B=A$时，$A\rightarrow B$也即$A\rightarrow A$，也就是$Th1$，那么有$\Gamma\vdash_{PC}A\rightarrow B$。

假设$k< n$时原命题成立，那么对于$B$的演绎序列中的公式有$\Gamma\vdash_{PC}A\rightarrow B_i,i< n$。

那么$k=n$时$B$或为公理、或有$B\in\Gamma\cup${$A$}，或由$B_i,B_j(i,j< n)$通过$r_{mp}$得到。

当$B$是公理时，$A\rightarrow B$有演绎序列$B,B\rightarrow(A\rightarrow B),A\rightarrow B$。

当$B\in\Gamma$时，$A\rightarrow B$有演绎序列$B,B\rightarrow(A\rightarrow B),A\rightarrow B$。

当$B=A$时，$A\rightarrow B$也即$A\rightarrow A$，也就是$Th1$，那么有$\Gamma\vdash_{PC}A\rightarrow B$。

当$B$由$B_i,B_j(i,j< n)$通过$r_{mp}$得到时，我们设$B_j=B_i\rightarrow B$。

那么有：$\Gamma\vdash_{PC}A\rightarrow B_i,\Gamma\vdash_{PC}A\rightarrow B_j$

也就是说：$\Gamma\vdash_{PC}A\rightarrow B_i,\Gamma\vdash_{PC}A\rightarrow(B_i\rightarrow B)$

由$A2$知：$(A\rightarrow(B_i\rightarrow B))\rightarrow((A\rightarrow B_i)\rightarrow(A\rightarrow B))$

故：$\vdash_{PC}(A\rightarrow B_i)\rightarrow(A\rightarrow B)$，则$\Gamma\vdash_{PC}A\rightarrow B$

我们现在回到上面那个例子，现在使用演绎定理解决这个问题。

证明：$\vdash_{PC}(A\rightarrow(B\rightarrow C))\rightarrow((C\rightarrow D)\rightarrow(A\rightarrow(B\rightarrow D)))$

即证：$A\rightarrow(B\rightarrow C)\vdash_{PC}(C\rightarrow D)\rightarrow(A\rightarrow(B\rightarrow D))$

即证：$A\rightarrow(B\rightarrow C),C\rightarrow D\vdash_{PC}A\rightarrow(B\rightarrow D)$

即证：$A\rightarrow(B\rightarrow C),C\rightarrow D,A\vdash_{PC}B\rightarrow D$

即证：$A\rightarrow(B\rightarrow C),C\rightarrow D,A,B\vdash_{PC}D$

1. $A$
2. $A\rightarrow(B\rightarrow C)$
3. $B\rightarrow C$,$r_{mp}(1)(2)$
4. $B$
5. $C$,$r_{mp}(3)(4)$
6. $C\rightarrow D$
7. $D$,$r_{mp}(5)(6)$

不难发现，在使用了演绎定理之后，我们的证明过程中涉及的公式变得更加简单了。

PC定理证明习题选

下面给出了六道PC定理习题供读者练习使用：

1. 证明：$\vdash_{PC}(A\rightarrow(B\rightarrow C))\rightarrow((A\rightarrow(D\rightarrow B))\rightarrow(A\rightarrow(D\rightarrow C)))$
2. 证明：$\vdash_{PC}(((A\rightarrow B)\rightarrow C)\rightarrow D)\rightarrow((B\rightarrow D)\rightarrow(A\rightarrow D))$
3. 证明：$\vdash_{PC}(A\rightarrow(\neg B\rightarrow(\neg D\rightarrow C)))\rightarrow((B\rightarrow\neg A)\rightarrow((C\rightarrow\neg A)\rightarrow(A\rightarrow D)))$
4. 证明：$\vdash_{PC}((D\rightarrow B)\rightarrow((C\rightarrow G)\rightarrow A))\rightarrow((E\rightarrow((C\rightarrow G)\rightarrow A))\rightarrow((D\rightarrow E)\rightarrow(G\rightarrow A)))$
5. 证明：$\vdash_{PC}(C\rightarrow(\neg A\rightarrow(\neg D\rightarrow A)))\rightarrow((B\rightarrow A)\rightarrow((\neg B\rightarrow C)\rightarrow(\neg A\rightarrow D)))$
6. 证明：$\vdash_{PC}((B\rightarrow C)\rightarrow(D\rightarrow E))\rightarrow(((B\rightarrow C)\rightarrow(G\rightarrow H))\rightarrow(((A\rightarrow B)\rightarrow C)\rightarrow\neg(((E\rightarrow G)\rightarrow(D\rightarrow H))\rightarrow\neg((G\rightarrow\neg H)\rightarrow\neg G))))$