有穷自动机FA及正则语言RL

前言

阅读本文需要集合论和图论的相关知识，在此不作有关集合论和图论相关知识的赘述。笔者水平有限，存在的错误和不足请大家指正。

字符串和语言

字母表（alphabet）：一个非空有穷集合，其成员被称为该字母表的符号（symbol），通常用大写希腊字母$\Sigma,\Gamma$来表示字母表和字母表中符号的打印字体。

字符串（string）：字母表中符号的有穷序列，通常写为一个符号挨着一个符号，不用逗号分隔，如果一个字符串$w$由字符$w_1,\cdots,w_n$一个挨着一个表示，称$w=w_1\cdots w_n$。一个字符串$w$所包含的符号数目称为它的长度（length），记作$|w|$。长度为零的字符串称为空串（empty string），记作$\epsilon$。若$\alpha$为$\alpha_1\cdots\alpha_m$、$\beta$为$\beta_1\cdots\beta_n$，它们都是某个字母表$\Sigma$的字符串，若$m=n$且对于每个$j,1\leq j\leq n$都有$\alpha_j$与$\beta_j$相同，称$\alpha=\beta$。

反转（reverse）：按照相反的顺序写$w$所得到的字符串，记作$w^R$，例如$w=w_1w_2\cdots w_n$，那么有$w^R=w_nw_{n-1}\cdots w_1$。

连接（concatenation）：若有字符串$x=x_1\cdots x_m,y=y_1\cdots y_n$，那么连接运算记作$xy=x_1\cdots x_my_1\cdots y_n$，也即把$y$附加在$x$得到的字符串。

不难发现全体字符串集$W$对连接运算构成了一个以字母表$\Sigma$为基的自由含幺半群/自由独异点，也即：

对于字符串$x,y,z\in W$，结合律$(xy)z=x(yz)$成立。
对于字符串$x\in W$，$\epsilon x=x\epsilon=x$，即$\epsilon$为单位元。
对于字符串$x\in W$，可以唯一地表示为$x=x_1\cdots x_n$，此处的$x_1,\cdots,x_n\in\Sigma$。
对于字符串$x,y,z\in W$，若有$xy=xz$，则$y=z$；若有$xz=yz$，则$x=y$。即满足左、右消去律。

因为结合律成立，可以定义一个字符串自身连接多次为$x^k=x\cdots x$，共有$k$个$x$连接。

子串（substring）：若有$\beta=\gamma\alpha\theta$，其中$\alpha,\beta,\gamma,\theta$都是某个字母表上的字符串，那么称$\alpha$为$\beta$的子串。

字典序（lexicographic order）：类似于大家熟悉的字典顺序，而一般采用字符串顺序（string order），它在字典序的基础上将短的字符串排在长的字符串的前面，例如字母表$\Sigma=${$0,1$}上的字符串顺序为$(\epsilon,0,1,00,01,10,11,000,\cdots)$。

前缀（prefix）：如果有字符串$x,y,z$满足$xz=y$，则称$x$是$y$的前缀，并且若$x\neq y$，则称$x$是$y$的真前缀（proper prefix）。

语言（language）：字符串的集合，称不含字符串的语言为空语言，记作$\varnothing$。如果语言中任何一个成员都不是其他成员的真前缀，那么该语言是无前缀的（prefix-free）。

有穷自动机

有穷自动机的引入

有穷自动机（finite automaton,FA） 是描述能力和资源极其有限的计算机的模型，但是它也可以做到很多的事情。以一个生活中的例子为例：

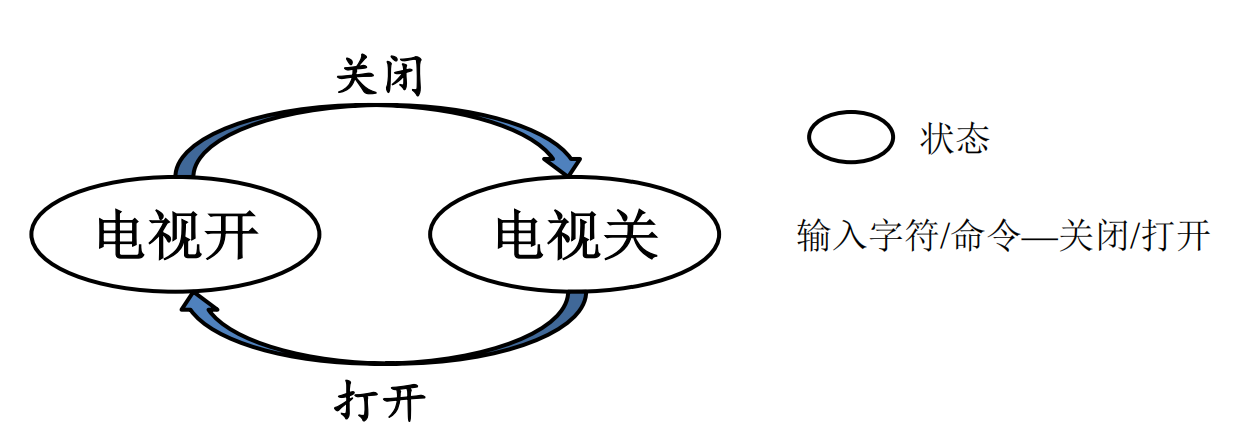
想象一个电视机，在处在开启状态时接收到关闭指令时它的状态会变为关闭，在处在关闭状态时接收到关闭指令时它的状态会变为开启，电视机有两个状态：开启状态和关闭状态，而指令是外部输入，这是一种有穷自动机。

一台电视机对应的自动机

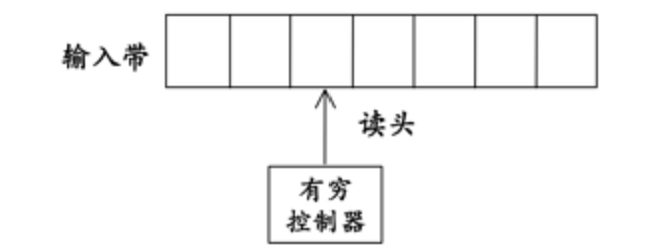
为了更好地描述FA，可以设想一种物理模型————FA的物理模型，现在对其进行描述。首先它带有一个输入带，在输入带上有一系列方格，每个方格里都储存了一个字符，约定输入串从输入带的左端点开始存放，而输入带的右端是无穷的。其次系统有一个有穷状态控制器（finite state control，FSC），带有有穷个状态，FSC控制了一个读头，每读入一个字符就将读头指向输入带的后一个字符。系统的运行按照3个节拍进行：读入读头指向的字符，FSC根据当前的状态和读入的字符改变状态，读头向右移动一格。

FA的物理模型示意图

而在很多地方FA都有它的应用，如在时序电路设计当中有摩尔机（Moore Machine）：时序电路的输出是现态的函数。米利机（Mealy Machine）：输出是现态和输入的函数。它们两个也都是FA,下面使用Verilog语言编写的三段式代码描述了一个时序电路中的Moore机，它包含在物理模型当中提到的读入输入，改变状态，等待下一个输入的过程。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


//状态寄存器
always @ (posedge clk or negedge rst_n) begin
    if(!rst_n)
        state <= IDLE;
    else
        state <= next_state;
end
//次态的组合逻辑
always @ (*) begin
    case(state)
        IDLE：begin
                if(w_i) next_state = S0;
                else   next_state = IDLE;
              end
        S0:  begin
                if(w_i) next_state = S1;
                else    next_state = IDLE;
             end
        S1:  begin
                if(w_i) next_state = S1;
                else    next_state = IDLE;
             end
        default : next_state = 2'bxx;
   endcase
end
//输出逻辑
always @ (*) beign
    case(current)
        IDLE:  z = 1'b0;
        S0:    z = 1'b0;
        S1:    z = 1'b1;
        default:  z = 1'b0;
    endcase
end

上面的这种FA也被称为有穷状态转换器（Finite-state transducer，FST），读者可以尝试自己给出它的形式化定义，在此不作相关说明。

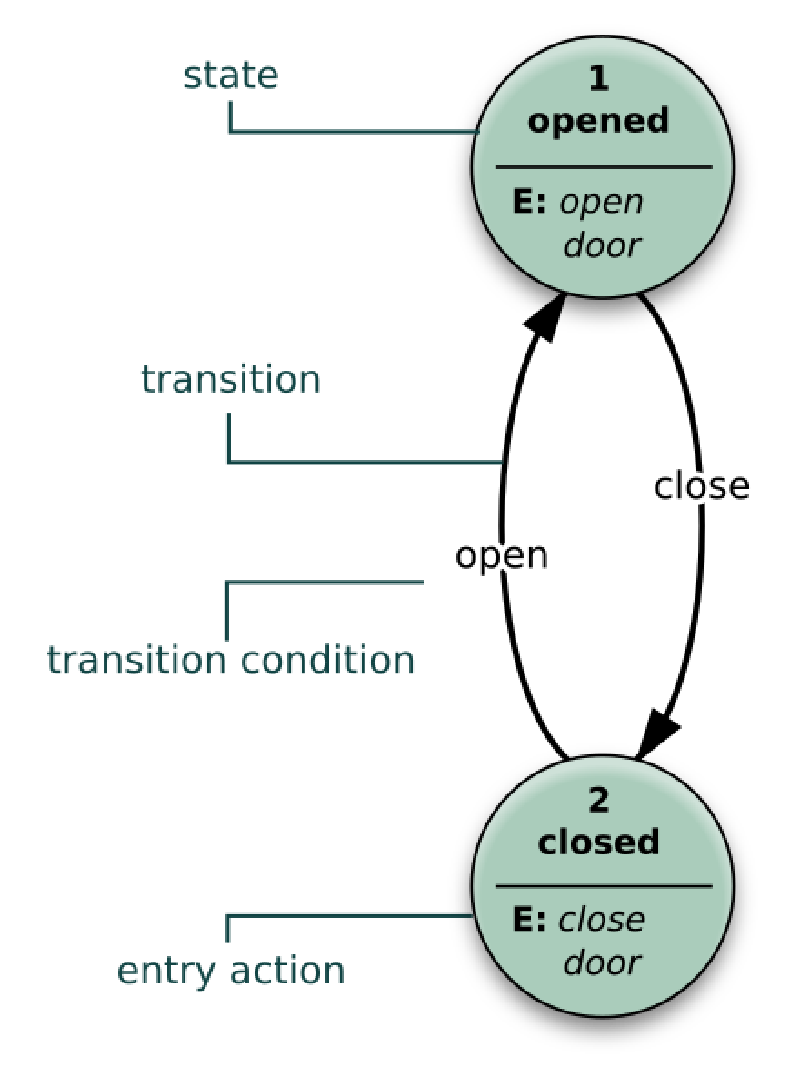
为了更好地描述FA的工作，先不给出FA的形式化定义，首先给出一个有穷自动机$M_1$：

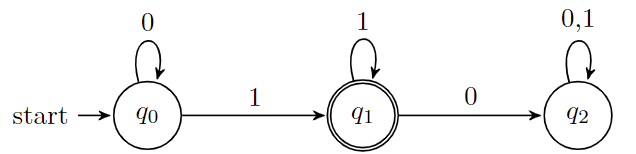
示例自动机

上面这个图被称为$M_1$的状态图（state diagram），它总共有三个状态$q_0,q_1,q_2$，起始状态（start state）$q_0$用一个单独的箭头表明出来，接受状态（accept state）$q_1$带有一个双圈，从一个状态指向另一个状态的箭头称为转移（transition）。当这个自动机接收到字符串后它会处理这个字符串并给出一个输出，或是接受或是拒绝。常用状态转移表来描述可能的转移过程：

	0	1
$q_0$	$q_0$	$q_1$
$q_1$	$q_2$	$q_1$
$q_2$	$q_2$	$q_2$

现在来看两个字符串输入的例子：

输入字符串011：

开始时处在状态$q_0$。

读到0，沿着转移从$q_0$到$q_0$。

读到1，沿着转移从$q_0$到$q_1$。

读到1，沿着转移从$q_1$到$q_1$。

输出接受，因为在输入字符串的末端$M$正处在一个接受状态$q_1$。

输入字符串1100：

开始时处在状态$q_0$。

读到1，沿着转移从$q_0$到$q_1$。

读到1，沿着转移从$q_1$到$q_1$。

读到0，沿着转移从$q_1$到$q_2$。

读到0，沿着转移从$q_2$到$q_2$。

输出拒绝，因为在输入字符串的末端$M$不处在一个接受状态。

有穷自动机的形式化定义

上面的例子说明，一台FA可以描述成一张含5个部分的表：状态集、输入字母表、动作规则、起始状态集和接受状态集。而用 转移函数（transition function） 来定义动作规则，常记作$\delta$。

FA是一个5元组$M=(Q,\Sigma,\delta,q_0,F)$，其中：

$Q$是一个有穷集合，称为状态集。
$\Sigma$是一个有穷集合，称为字母表。
$\delta:Q\times\Sigma\rightarrow Q$，称为转移函数。
$q_0\in Q$是起始状态。
$F\subseteq Q$是接受状态集。

这样就可以给出上面的例子$M_1$的形式化描述：

$Q=${$q_0,q_1,q_2$}。

$\Sigma=${$0,1$}。

$\delta(q_0,0)=q_0,\delta(q_0,1)=q_1,\delta(q_1,0)=q_2,\delta(q_1,1)=q_1,\delta(q_2,0)=q_2,\delta(q_2,1)=q_1$。

$q_0$是起始状态。

$F=${$q_1$}。

若$A$是机器$M$所接受的全部字符串集，则称$A$是机器$M$的语言，记作$L(M)=A$，又称$M$识别$A$或$M$接受$A$。

转移函数处理的是一个字符，为了在理论分析时更加便于处理字符串，定义扩展转移函数$\hat{\delta}$：当$w=\epsilon$时$\hat{\delta}(q,w)=q$，当$w=xa$时$\hat{\delta}(q,w)=\delta(\hat{\delta}(q,x),a)$，其中$w,x$是字符串，$a$是字符。可知机器$M$接受$w$当且仅当$\hat{\delta}(q_0,w)\in F$。

正则运算

正则语言（regular language，RL）：如果一个语言被一台FA识别，则称它为正则语言。

为了更好的研究RL，引入 正则运算（regular operation） 以便研究它的性质，设$A,B$为两个语言，那么有：

并（union）：$A\cup B=${$x|x\in A或x\in B$}，也有写作$A+B$的。
连接（concatenation）：$A\circ B=${$xy|x\in A且y\in B$}，在不产生混淆的情况下可以写为$AB$。
幂（power）：$A^0=${$\epsilon$}$,A^1=A,A^n=A^{n-1}\circ A$。
克林闭包（Kleene star）：$A^{ * }=\cup^\infty_{i=0}A^i$，也有一种定义称$A^+=\cup^\infty_{i=1}A^i$为正闭包。

除了正则运算外，也有一些常用的运算，在此也作出介绍：

对于两个语言$A,B$，那么有交运算：$A\cap B=${$x|x\in A且x\in B$}。
对于两个语言$A,B$，那么有差运算：$A-B=${$x|x\in A且x\notin B$}。
对于字母表$\Sigma$上的一个语言$L$，称这个语言的补运算为：$\overline{L}=\Sigma^{ * }-L$，显然有$L-M=L\cap\overline{M}$。
对于字母表$\Sigma$上的语言$L$，称它的反转为$L^R=${$w^R\in\Sigma^{ * }|w\in L$}。
对于字母表$\Sigma$上的语言$L_1,L_2$，称**商（quotient）**为：$L_1/L_2=${$x|\exists y\in L_2使得xy\in L_1$}，这里是$L_2$除以$L_1$的商。

为了更好地研究语言和运算之间的性质，引入封闭性的概念：

如果任意的属于某一语言类的语言在某一特定运算下所得的结果任然是该类语言，则称该语言类对此运算是封闭的，并称该语言类对此运算有封闭性（closure property）。

给定一个语言类的若干语言的描述。如果存在一个算法，它可以构造出这些语言在给定运算下所获得的运算结果的相应形式的语言描述，则称此语言类对相应的运算是有效封闭的，并称此语言类对相应的运算具有有效封闭性（valid closure property）。

可以证明RL在并运算下是封闭的：

设有RL：$A_1,A_2$，识别它们的有穷状态机分别为$M_1=(Q_1,\Sigma,\delta_1,q_1,F_1),M_2=(Q_2,\Sigma,\delta_2,q_2,F_2)$（两者的字母表不同时也可以构造相应的证明过程），那么可以构造这样一台FA$M=(Q_1\times Q_2,\Sigma,\delta,(q_1,q_2),(F_1\times Q_2)\cup(Q_1\times F_2))$，其中对于每一对$(r_1,r_2)\in Q,a\in\Sigma$，$\delta((r_1,r_2),a)=(\delta_1(r_1,a),\delta_2(r_2,a))$，这台自动机可以识别$A_1\cup A_2$。

RL在连接运算下也是封闭的，但是如果想要证明这个事实，就会面临一个问题，该如何让需要构造的自动机$M$知道哪里才能将输入的字符串$w=w_1w_2$分为$w_1$和$w_2$，从而让两者分别被两台自动机接受呢？为了解决这个问题要引入非确定性。

非确定性

非确定性的引入

在刚刚定义的FA可以被称为确定的有穷自动机（deterministic finite automaton,DFA），它进行的是确定性计算（deterministic computation），现在要介绍的是带空移动的不确定的有穷自动机（non-deterministic finite automaton with $\epsilon$,$\epsilon$-NFA），这种机器是前者的推广，而在任何一点，其下一个状态可能存在若干个选择。

首先给出一个$\epsilon$-NFA的例子，记其为$N_1$：

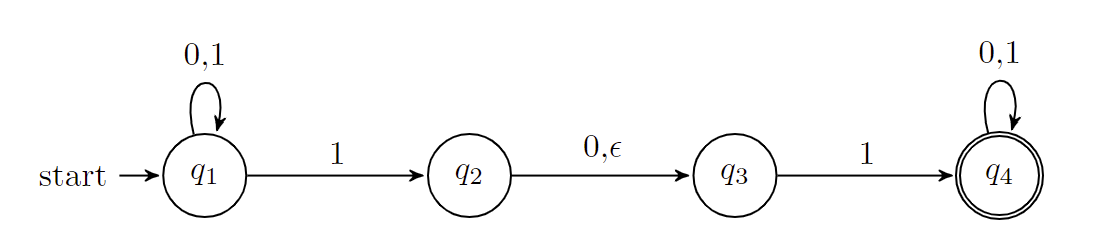
示例自动机

与DFA相比，这里某些状态对字母表中的某些符号产生了多个转移箭头，也有些符号没有对应的转移箭头，而这里出现了不取自于字母表的符号$\epsilon$。一般而言，$\epsilon$-NFA的箭头可以标记为字母表中的元素或$\epsilon$，从一个状态可能射出0个、1个或若干个标有$\epsilon$的箭头。

$\epsilon$-NFA进行运算的过程像是多线程工作，当读入一个字符对应多个转移箭头时，$\epsilon$-NFA便会“复制”自己以进行多个方向的工作，当没有可以转移的箭头时这个$\epsilon$-NFA的“备份”便结束工作，而遇到带有$\epsilon$的箭头时$\epsilon$-NFA直接“复制”一份自身进行工作，也可以借助树的结构来观察这个过程。

以$N_1$为例，输入字符串010110：

开始时处在状态$q_1$。

读到0，沿着转移从$q_1$到$q_1$。

读到1，沿着转移从$q_1$到$q_1,q_2,q_3$。

读到0，沿着转移从$q_1$到$q_1$，从$q_2$到$q_3$，$q_3$无法进行转移。

读到1，沿着转移从$q_1$到$q_1,q_2,q_3$，从$q_3$到$q_4$。

读到1，沿着转移从$q_1$到$q_1,q_2,q_3$，从$q_3$到$q_4$，从$q_3$到$q_4$，$q_2$无法进行转移。

读到0，沿着转移从$q_1$到$q_1$，从$q_2$到$q_3$，从$q_4$到$q_4$，$q_3$无法进行转移。

输出接受，因为存在一个NFA的“备份”能够到达接受状态$q_4$。

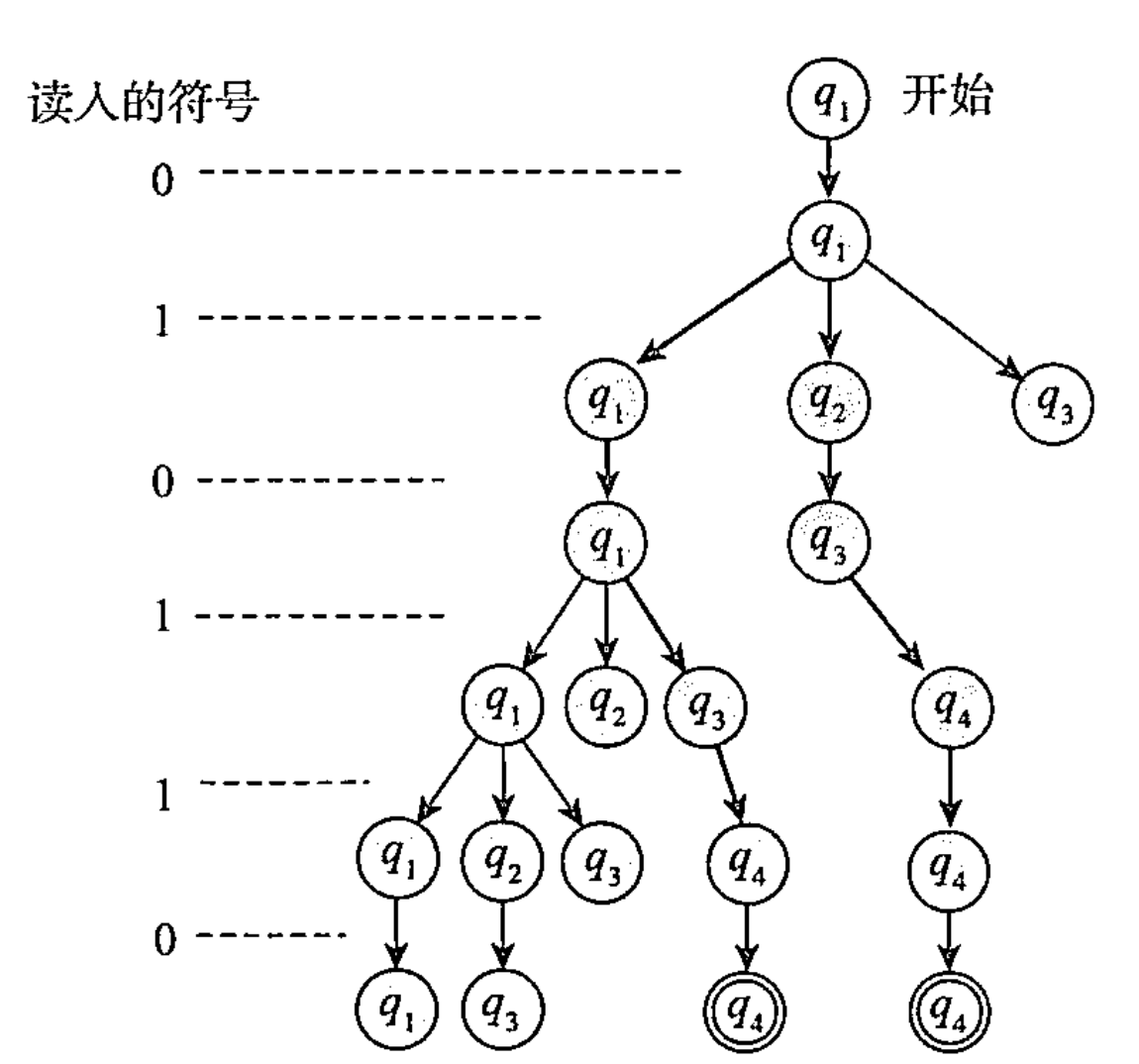
利用树的结构来观察这个过程如下：输入字符串后自动机的状态转移示意图

非确定性的形式化定义

现在给出$\epsilon$-NFA的形式化定义，$\epsilon$-NFA是一个五元组$(Q,\Sigma,\delta,q_0,F)$：

$Q$是一个有穷集合，称为状态集。
$\Sigma$是一个有穷集合，称为字母表。
$\delta:Q\times\Sigma_\epsilon\rightarrow 2^Q$，称为转移函数，其中$2^Q$表示$Q$的幂集，即$Q$的全体子集的集合，$\Sigma_\epsilon=\Sigma\cup${$\epsilon$}。
$q_0\in Q$是起始状态。
$F\subseteq Q$是接受状态集。

当$\epsilon$-NFA中不含有有$\epsilon$的转移箭头时得到了 不确定的有穷自动机（non-deterministic finite automaton,NFA） 的定义，在此不作赘述。

为了方便研究，引入$\epsilon$-闭包（$\epsilon$-Closure）的概念，记为$ECLOSE(q)$，表示经过0个或多于0个空转移到达的全部状态的集合，其递归定义如下：

$q\in ECLOSE(q)$（包含当前状态本身）

$\forall p\in ECLOSE(q),$如果有$r\in\theta(p,\epsilon)$，那么$r\in ECLOSE(q)$。

在$N_1$中可以发现$ECLOSE(q_0)=${$q_0$}$,ECLOSE(q_1)=${$q_1,q_2$}。

对$\epsilon$-闭包进行推广，状态集$S$的$\epsilon$-闭包为：$ECLOSE(S)=\cup_{q\in S}ECLOSE(q)$，即一个状态集$S$的$\epsilon$-闭包为$S$中每一个状态的$\epsilon$-闭包的并集。

类似于先前做的那样，也给出扩展转移函数$\hat{\delta}$：

$\hat{\delta}$：当$w=\epsilon$时$\hat{\delta}(q,w)=ECLOSE(q)$，当$w=xa$时$\hat{\delta}(q,w)=ECLOSE(\cup_{p\in\hat{\delta}(q,x)}\delta(p,a))$，其中$w,x$是字符串，$a$是字符。可知机器$N$接受$w$当且仅当$\hat{\delta}(q_0,w)\cap F\neq\varnothing$。

DFA和ε-NFA的等价性

当两台机器识别同样的语言，则称它们是等价的，乍一看上去仿佛$\epsilon$-NFA有着比DFA更加强大的能力，因为DFA本身便符合$\epsilon$-NFA的定义，但是两者实际上是等价的，为此，需要找到用DFA表示$\epsilon$-NFA的方法，这样的构造如下：

设有$\epsilon$-NFA：$N=(Q,\Sigma,\delta,q_0,F)$，其识别了语言$A$，那么可以构造一台DFA识别语言$A$：$D=(2^Q,\Sigma,\delta_D,ECLOSE(q_0),F_D)$，其中$\forall S\subseteq Q,\forall a\in\Sigma,\delta_D(S,a)=ECLOSE(\cup_{p\in S}\delta(p,a))$，$F_D=${$S|S\subseteq Q,S\cap F\neq\varnothing$}。

NFA是$\epsilon$-NFA的特殊情形，同时DFA一定是NFA，故这三种FA都是等价的。

知道了两者的等价性后，可以得到推论：一个语言是正则的当且仅当有一台$\epsilon$-NFA可以识别它。

在正则运算下的封闭性

有了关于$\epsilon$-NFA的知识后，可以回过头来看看之前所未解决的问题，也即证明RL在正则运算下的封闭性，在此通过构造三个$\epsilon$-NFA将这个问题解决：

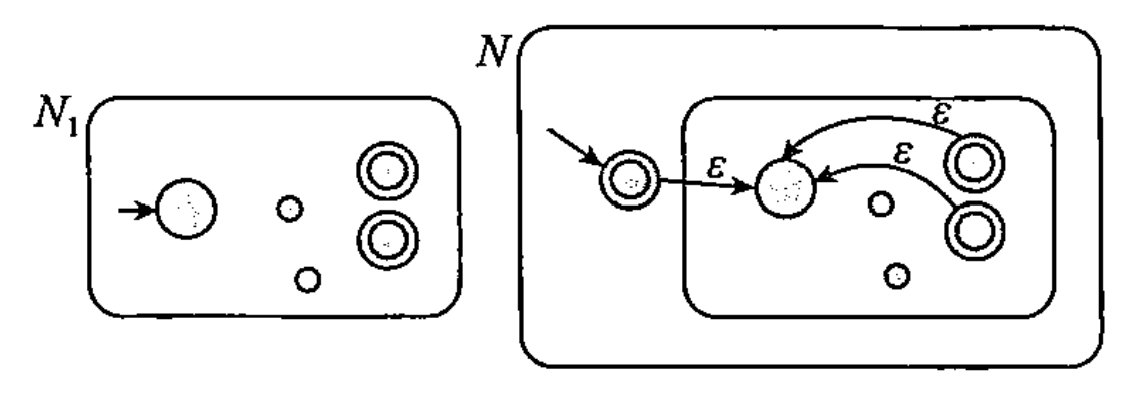
（1）正则语言在并运算下封闭：

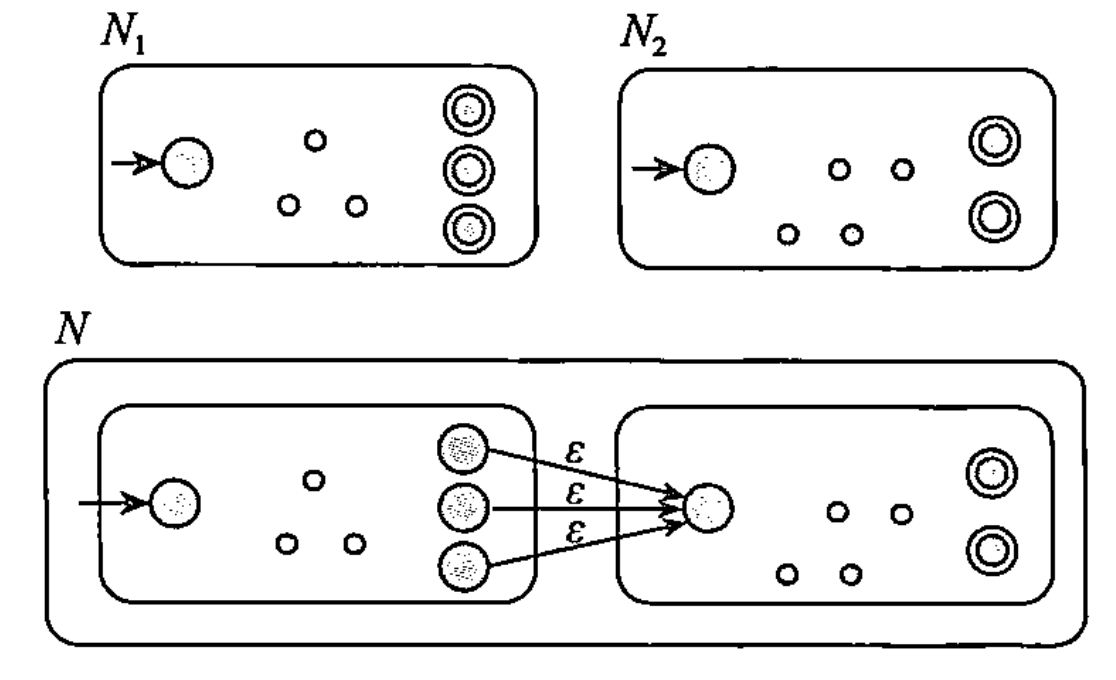
设有RL：$A_1,A_2$被它们对应的两个$\epsilon$-NFA识别：$N_1=(Q_1,\Sigma,\delta_1,q_1,F_1),N_2=(Q_2,\Sigma,\delta_2,q_2,F_2)$，那么可以识别$A_1\cup A_2$的$\epsilon$-NFA构造为：$N=(${$q_0$}$\cup Q_1\cup Q_2,\Sigma,\delta,q_0,F_1\cup F_2)$，其中$\forall q\in Q,a\in \Sigma_\epsilon$

当$q\in Q_1$时$\delta(q,a)=\delta_1(q,a)$

当$q\in Q_2$时$\delta(q,a)=\delta_2(q,a)$

当$q=q_0$且$a=\epsilon$时$\delta(q,a)=${$q_1,q_2$}

当$q=q_0$且$a\neq\epsilon$时$\delta(q,a)=\varnothing$

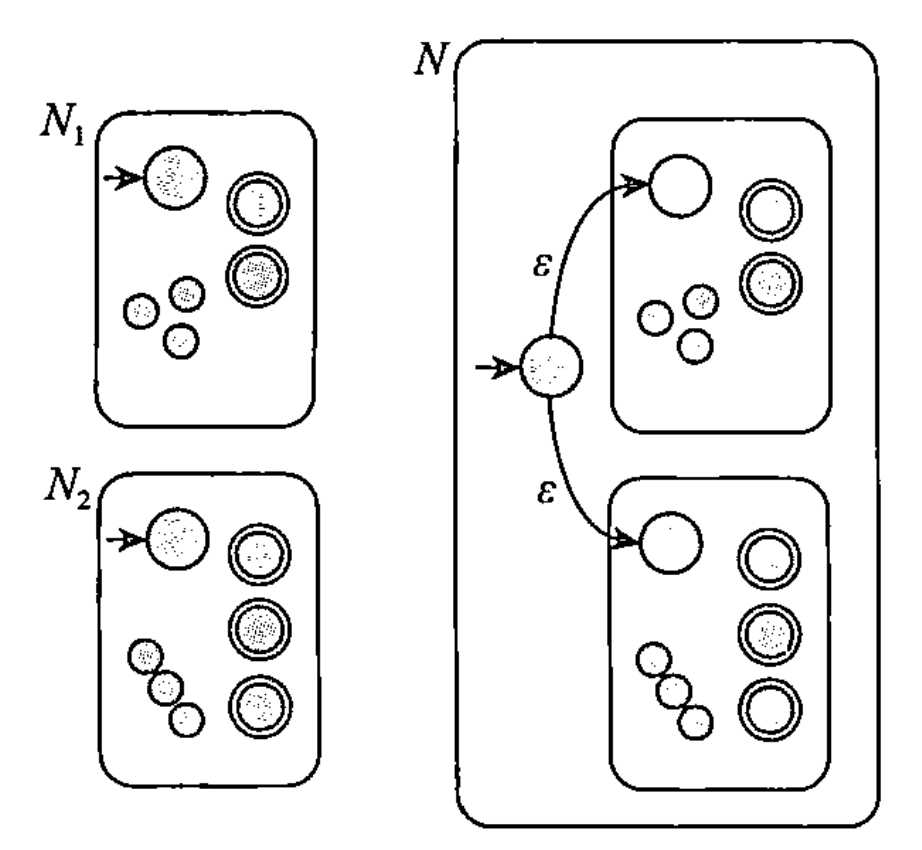
并运算对应的自动机

（2）正则语言在连接运算下封闭：

设有RL：$A_1,A_2$被它们对应的两个$\epsilon$-NFA识别：$N_1=(Q_1,\Sigma,\delta_1,q_1,F_1),N_2=(Q_2,\Sigma,\delta_2,q_2,F_2)$，那么可以识别$A_1\circ A_2$的$\epsilon$-NFA构造为：$N=(Q_1\cup Q_2,\Sigma,\delta,q_1,F_2)$，其中$\forall q\in Q,a\in \Sigma_\epsilon$

当$q\in Q_1$且$q\notin F_1$时$\delta(q,a)=\delta_1(q,a)$

当$q\in F_1$且$a\neq\epsilon$时$\delta(q,a)=\delta_1(q,a)$

当$q\in F_1$且$a=\epsilon$时$\delta(q,a)=\delta_1(q,a)\cup${$q_2$}

当$q\in Q_2$时$\delta(q,a)=\delta_2(q,a)$

（3）正则语言在克林闭包运算下封闭：

设有RL：$A_1$被对应的$\epsilon$-NFA识别：$N_1=(Q_1,\Sigma,\delta_1,q_1,F_1)$，那么可以识别$A_1^{ * }$的$\epsilon$-NFA构造为：$N=(${$q_0$}$\cup Q_1,\Sigma,\delta,q_0,${$q_0$}$\cup F_1)$，其中$\forall q\in Q,a\in \Sigma_\epsilon$

当$q\in Q_1$且$q\notin F_1$时$\delta(q,a)=\delta_1(q,a)$

当$q\in F_1$且$a\neq\epsilon$时$\delta(q,a)=\delta_1(q,a)$

当$q\in F_1$且$a=\epsilon$时$\delta(q,a)=\delta_1(q,a)\cup${$q_1$}

当$q=q_0$且$a=\epsilon$时$\delta(q,a)=${$q_1$}

当$q=q_0$且$a\neq\epsilon$时$\delta(q,a)=\varnothing$

克林闭包运算对应的自动机

在其他运算下的封闭性

RL除了在这些正则运算下保持封闭，在其他运算下也有保持封闭的性质，在此选取了常用的性质进行说明：

（1）RL在补运算下封闭：

设有RL：$A$被对应的DFA识别：$D=(Q,\Sigma,\delta,q_0,F)$，那么可以识别$\overline{L}=\Sigma^{ * }-L$的DFA构造为$D’=(Q,\Sigma,\delta,q_0,Q-F)$。

（2）RL在交运算下封闭：

如果$L,M$是RL，考虑事实$L\cap M=\overline{\overline{L}\cup\overline{M}}$。

也可以通过构造自动机证明这一事实，设有RL：$A_1,A_2$被对应的两个DFA识别：$M_1=(Q_1,\Sigma,\delta_1,q_1,F_1),M_2=(Q_2,\Sigma,\delta_2,q_2,F_2)$，那么可以构造识别$A_1\cap A_2$的DFA：$M=(Q_1\times Q_2,\Sigma,\delta,(q_1,q_2),F_1\times F_2)$。其中$\forall (p,q)\in Q_1\times Q_2,\forall a\in\Sigma,\delta((p,q),a)=(\delta_1(p,a),\delta_2(q,a))$。

（3）RL在差运算下封闭：

如果$L,M$是RL，考虑事实$L-M=L\cap\overline{M}$。

（4）RL在反转运算下封闭：

设有RL：$A$被相应的DFA：$D=(Q,\Sigma,\delta,q_0,F)$识别，可以构造识别$A^R$的$\epsilon$-NFA：$N=(Q,\Sigma,\delta’,q_R,${$q_0$}$)$，如果有$\delta(q,a)=p$，那么作$\delta’(p,a)=q$，同时要求$\delta’(q_R,\epsilon)=F$，恰好满足这两个条件即可。

（5）正则代换：

可以引入代换（substitution） 的概念，设有两个字母表$\Sigma,\Delta$，那么映射$f:\Sigma\rightarrow 2^{\Delta^{ * }}$称为从$\Sigma$到$\Delta$的一个代换，如果对于$\forall a\in\Sigma,f(a)$是$\Delta$上的RL，则称$f$为正则代换（regular substitution）。

可以进一步扩展$f$的定义域，首先将其定义域拓展到$\Sigma^{ * } $上，也就是说定义字符串的代换，$f:\Sigma^{ * }\rightarrow 2^{\Delta^{ * }}$：

$f(\epsilon)=${$\epsilon$}。
$f(xa)=f(x)f(a)$。

再将定义域拓展到$2^{\Sigma^{ * } }$上，也就是定义语言的代换，$f:2^{\Sigma^{ * }}\rightarrow 2^{\Delta^{ * } }$：对于$\forall L\subseteq\Sigma^{ * } $，有$f(L)=\cup_{x\in L}f(x)$。为了方便研究，也给出正则表达式上的正则代换：设$\Sigma,\Delta$是两个字母表，映射$f:\Sigma\rightarrow 2^{\Delta^{ * }}$为正则代换，那么有：

$f(\varnothing)=\varnothing$。
$f(\epsilon)=\epsilon$。
对于$\forall a\in\Sigma,f(a)$是$\Delta$上的正则表达式
如果$r,s$是$\Sigma$上的正则表达式，那么有:$f(r\cup s)=f(r)\cup f(s),f(r\circ s)=f(r)\circ f(s),f(r^{ * })=f(r)^{ * }$。

使用数学归纳法很容易证明：设$L$是$\Sigma$上的一个RL，有正则代换$f:\Sigma\rightarrow 2^{\Delta^{ * }}$，则$f(L)$也是RL。

可以引入 同态（homomorphism） 的概念，设有两个字母表$\Sigma,\Delta$，有映射$f:\Sigma\rightarrow\Delta^{ * } $。如果对于$\forall x,y\in\Sigma^{ * } $有$f(xy)=f(x)f(y)$，则称$f$为从$\Sigma$到$\Delta^{ * } $的同态映射。

对于$\forall L\subseteq\Sigma^{ * }$，$L$的同态像$f(L)=\cup_{x\in L}${$f(x)$}。

对于$\forall w\subseteq\Delta^{ * } $，$w$的同态原像$f^{-1}(w)=${$x|f(x)=w且x\in\Sigma^{ * }$}。

对于$\forall L\subseteq\Delta^{ * } $，$L$的同态原像$f^{-1}(L)=${$x|f(x)\in L$}。

（6）RL在同态像运算下封闭：

不难发现同态映射是正则代换的特例。

（7）RL在同态原像运算下封闭：

设有$L$是RL，有同态映射$h:\Sigma\rightarrow\Delta^{ * } $，识别它的DFA：$D=(Q,\Gamma,\delta,q_0,F)$，那么可以构造识别$h^{-1}(A)$的DFA：$D’=(Q,\Sigma,\delta’,q_0,F)$，其中对$\forall (q,a)\in Q\times\Sigma$，都有$\delta’(q,a)=\delta(q,h(a))$。

（8）RL在商运算下封闭:

设$L_1,L_2\in\Sigma^{ * } $，如果$L_1$是RL，则$L_1/L_2$也是RL。设有识别$L_1$的DFA：$M_1=(Q,\Sigma,\delta,q_0,F_1)$，那么可以构造识别$L_1/L_2$的DFA：$M_2=(Q,\Sigma,\delta,q_0,${$q|\exists y\in L_2,\delta(q,y)\in F$}$)$。

必须要指出的是，这里的$L_2$可以是各种语言，故这种封闭性不是有效封闭性。

正则表达式

正则表达式的形式化定义

正则表达式（regular expression，RE）：类似于算术中的运算存在着对应的表达式，如$5+4$，也可以使用正则运算描述语言的表达式，称为正则表达式，例如$(0\cup 1)0^{ * }$，现在给出它的形式化定义：

称$R$是一个正则表达式，如果$R$是：

$a$，要求$a\in\Sigma$，$\Sigma$是字母表，表示语言{$a$}。
$\epsilon$，表示语言{$\epsilon$}。
$\varnothing$，表示空语言。
$(R_1\cup R_2)$，其中$R_1,R_2$都是正则表达式，表示这两个语言作并运算得到的语言，也有写成$(R_1+R_2)$的。
$(R_1\circ R_2)$，其中$R_1,R_2$都是正则表达式，表示这两个语言作连接运算得到的语言，在不产生混淆的情况下可以写为$(R_1R_2)$。
$(R_1)^{ * }$，其中$R_1$是正则表达式，表示这个语言作克林闭包运算得到的语言。

上述的定义是有效的、可以避免循环的，被称为归纳定义（inductive defination）。

表达式中的括号可以被略去，如果略去括号，可以按照下述优先顺序进行运算：克林闭包，连接，并。

正则表达式$R$所描述的语言记作$L(R)$。

正则表达式和这里使用到的三种运算形成了Kleene代数（例如对并运算和连接运算形成了一个半环），在此指出有关正则表达式的一些代数定律：

并运算满足交换律和结合律。
连接运算满足结合律，但不满足交换律。
$\varnothing$是并运算的单位元，是连接运算的零元，也就是说对于正则表达式$L$始终有$\varnothing\cup L=L\cup\varnothing=L,\varnothing\circ L=L\circ\varnothing=\varnothing$。
$\epsilon$是连接运算的单位元，也就是说对于正则表达式$L$始终有$\epsilon L=L\epsilon =L$。
连接运算对并运算满足左右分配律。
并运算满足幂等律。
对任意语言$L$都有$(L^{ * })^{ * }=L^{ * }$。
$\varnothing^{ * }=\epsilon$。
$\epsilon^{ * }=\epsilon$。
对任意语言$L$都有$L^{ * }L^{ * }=L^{ * }$。
对任意语言$L,M$都有$(L\cup M)^{ * }=(L^{ * }M^{ * })^{ * }$。

与有穷自动机的等价性

现在要说明一个正则语言一定可以用正则表达式描述，反之亦然，也就是说要证明两个命题，下面给出这两个命题的证明。

（1）如果一个语言可以用正则表达式描述，那么它是正则的。

可以使用归纳法证明这个结论，归纳基础如下：

归纳基础

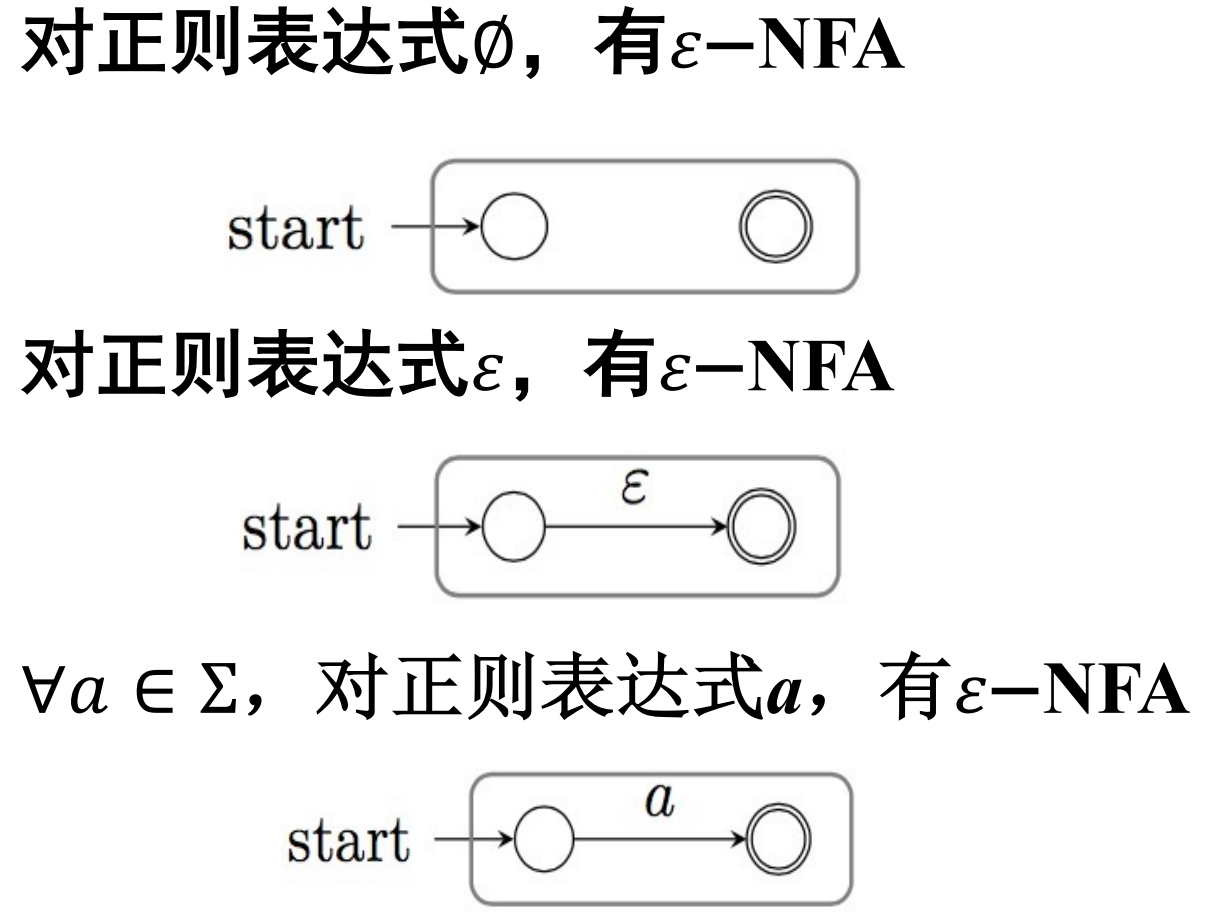
归纳递推如下：

归纳递推

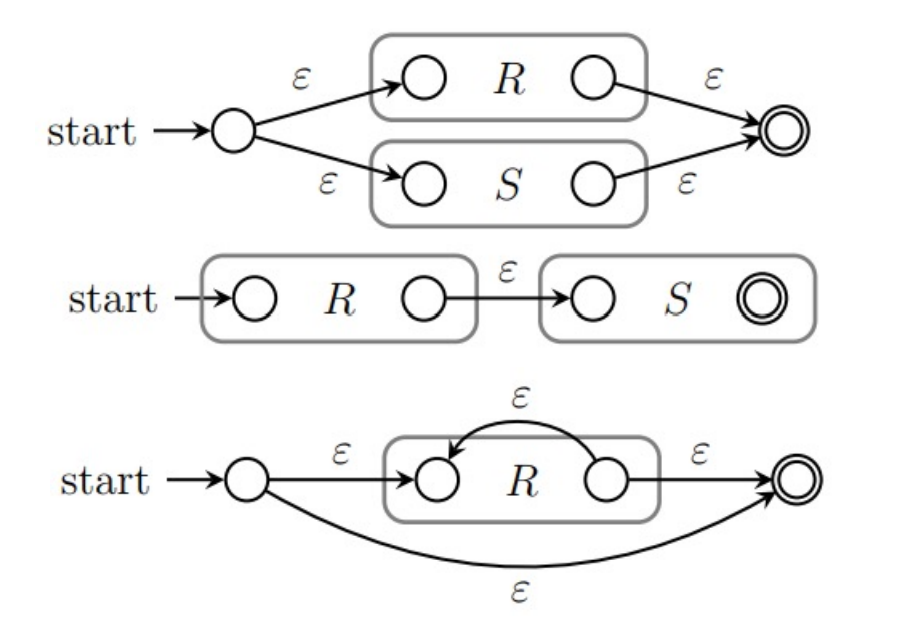
这样的三种构造恰好可以与三种正则运算相对应

那么找到了将正则表达式转化为对应的$\epsilon$-NFA的方法，证明完毕。

（2）如果一个语言是正则的，那么可以用正则表达式描述它。

首先，给出一种方法证明这个问题，设有DFA：$M=(\cup_{i=1}^n${$q_i$}$,\Sigma,\delta,q_1,F)$

令$R^k_{ij}=${$x|\hat{\delta}(q_i,x)=q_j,而且对于x的任意前缀y(y\neq x,y\neq\epsilon),如果\hat{\delta}(q_i,y)=q_j,则l\leq k$}

也就是说$R^k_{ij}$是所有那些将DFA从给定状态$q_i$引导到状态$q_j$并且中途不经过下标大于$k$的状态的那些字符串，可以发现有递归关系：

如果$i\neq j$那么有$R^0_{ij}=${$a|\hat{\delta}(q_i,a)=q_j$}，如果$i=j$那么有$R^0_{ij}=${$a|\hat{\delta}(q_i,a)=q_j$}$\cup${$\epsilon$}。

$R^k_{ij}=R^{k-1}{ik}(R^{k-1}{kk})^{ * } R^{k-1}{kj}\cup R^{k-1}{ij}$

显然有$L(M)=\cup_{q_j\in F}R^n_{1f}$。

上述这种做法不太直观，为此可以通过引入一个新的自动机：广义非确定型有穷自动机（generalized nondeterministic finite automaton，GNFA） 来解决这个问题，下面给出一个例子对这种自动机进行说明：

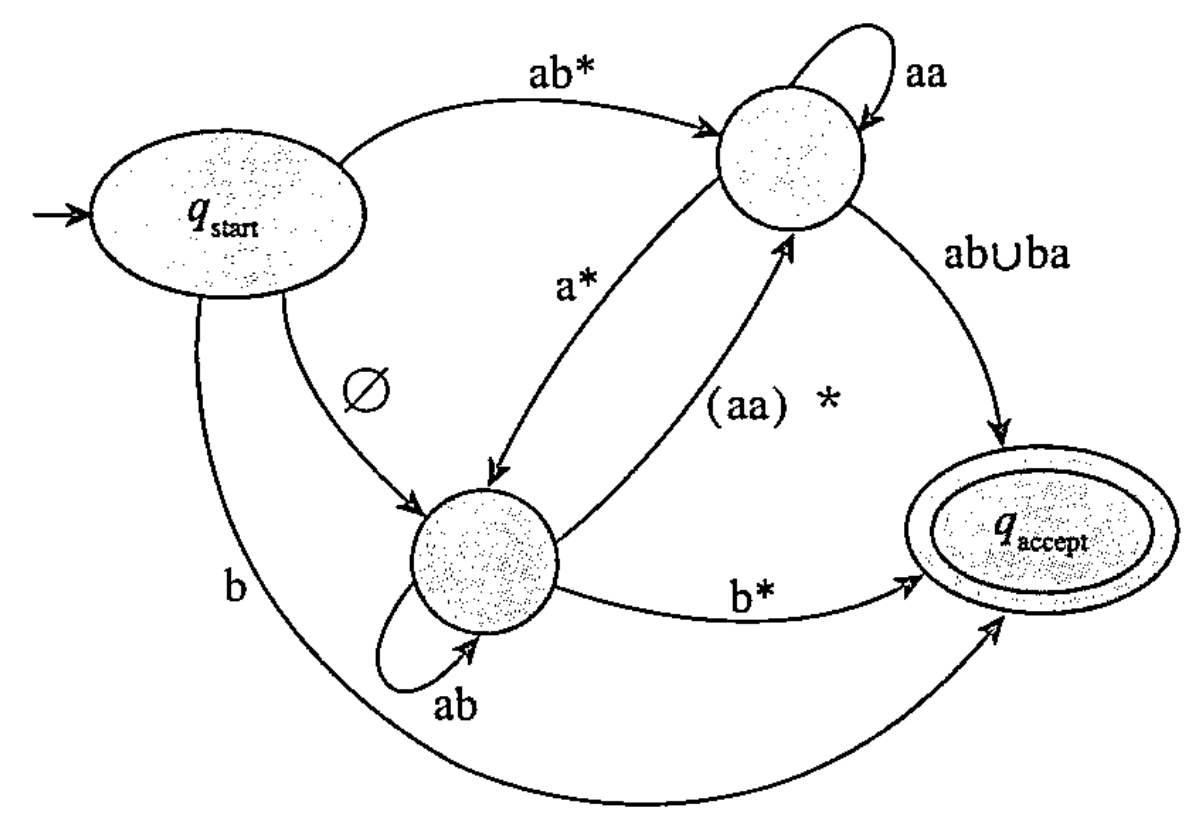
一台GNFA

可以发现GNFA的转移箭头可以用任何正则表达式作标号，而不是只能用字母表的成员或者$\epsilon$作为标号。相较于NFA一次最多只能读入一个符号，GNFA可以一次读入一段输入符号，沿着连接两个状态的箭头移动，而这段输入符号正好是那个转移箭头上的正则表达式所描述的一个字符串。

为了方便，对GNFA作出一些特殊形式的条件要求：

起始状态有射到其他每一个状态的箭头，但是没有从任何其他状态射入的箭头。
有唯一的接受状态，并且它有从其他每一个状态射入的箭头，但是没有射到任何其他状态的箭头。此外，这个接受状态和起始状态不同。
除了起始状态和接受状态之外，每一个状态到自身和其他每一个状态都有一个箭头。

把DFA转换成GNFA是容易的，只需要新添加初始状态和接受状态，新初始状态到原初始状态有一个$\epsilon$箭头，每一个原接受状态到新接受状态有一个$\epsilon$箭头，把有多个标记的箭头换成并运算的正则表达式形式，最后将需要补上箭头的原先无箭头的地方补上$\varnothing$的箭头即可，因为这个箭头始终无法被使用。

现在给出GNFA的形式化定义：

广义非确定型有穷自动机是一个5元组$(Q,\Sigma,\delta,q_{start},q_{accept})$

$Q$是一个有穷的状态集。
$\Sigma$是一个有穷的字母表。
$\delta:(Q-${$q_{accept}$}$)\times(Q-${$q_{start}$}$)\rightarrow \mathcal{R} $，即转移函数。
$q_{start}\in Q$是起始状态。
$q_{accept}$是接受状态。

如果字符串$w=w_1w_2\cdots w_k$，其中的每一个$w_i\in\Sigma^{ * }$，并且存在状态序列$q_0,q_1,\cdots,q_k$使得

$q_0=q_{start}$是起始状态。
$q_k=q_{accept}$是接受状态。
对于每一个$i,w_i\in L(R_i)$，其中$R_i=\delta(q_{i-1},q_i)$，即$R_i$是从$q_{i-1}$到$q_i$的箭头上的正则表达式。

那么称这个GNFA接受字符串$w$。

而对于GNFA，存在一种算法可以不断减少它所拥有的状态数目，最后将会剩下它的初始状态和接受状态，同时也只有一个从初始状态到接受状态的箭头，这个箭头的标记就说等价的正则表达式，现在给出这样一个算法CONVERT(G)，它通过每轮减少一个状态的方式实现了状态的缩减：

设$k$为$G$的状态数，如果$k=2$则$G$一定是一个起始状态、一个接受状态和连接两者的箭头组成，返回箭头上标记的正则表达式$R$。

如果$k>2$，则任取一个状态$q_{rip}\in Q-${$q_{start},q_{accept}$}，并且令一个新的GNFA：$G’=(Q’,\Sigma,\delta’,q_{start},q_{accept})$，其中$Q’=Q-${$q_{rip}$}，而对于每一个$q_i\in Q’-${$q_{accept}$}$,q_j\in Q’-${$q_{start}$}，令$\delta’(q_i,q_j)=(R_1)(R_2)^{ * }(R_3)\cup(R_4)$，其中$R_1=\delta(q_i,q_{rip}),R_2=\delta(q_{rip},q_{rip}),R_3=\delta(q_{rip},q_j),R_4=\delta(q_i,q_j)$，计算CONVERT(G)并返回这个值。

实际上当$k>2$时CONVERT(G)所做的事情是将某个状态去掉，用能够经过这个状态的路径对应的正则表达式取代了它，从而不影响整个状态机的运行。

可以证明对于任意的GNFA G，都有CONVERT(G)等价于G，也就是说所有GNFA都有与其等价的一个含有两个状态的GNFA。证明了任何RL都可以用正则表达式来描述它。

Myhill-Nerode定理和DFA的极小化

Myhill-Nerode定理

知道任何GNFA都可以被化简为只有两个状态的形式，但是这不意味着DFA和$\epsilon$-NFA可以被化简为只有两个状态的形式，实际上总能找到这样的语言$L_n$使得能够接受它的DFA和$\epsilon$-NFA拥有至少$n$个状态（考虑只含有一个字符串的形如{$0^k$}的语言）。

但是可以对这些自动机进行化简，在此给出减少DFA的状态以化简它的方法。

设DFA：$M=(Q,\Sigma,\delta,q_0,F)$，由$M$确定的$\Sigma^{ * } $上的关系$R_M$定义为：对于$\forall x,y\in\Sigma^{ * } $都有$xR_My\Leftrightarrow\hat{\delta}(q_0,x)=\hat{\delta}(q_0,y)$。

设$L\subseteq\Sigma^{ * } $，$L$确定的$\Sigma^{ * } $上的关系$R_L$定义为：对于$\forall x,y\in\Sigma^{ * } $，$xR_Ly\Leftrightarrow(对\forall z\in\Sigma^{ * } ,xz\in L\Leftrightarrow yz\in L)$。可以证明$xR_My\Rightarrow xR_{L(M)}y$，但是反之不成立。

设$R$是$\Sigma^{ * } $上的等价关系，对于$\forall x,y\in\Sigma^{ * } $，如果$xRy$则$\forall z\in\Sigma^{ * } $都有$xzRyz$，那么称$R$是右不变的（right invariant） 等价关系。可以证明上面定义的两个关系都是右不变的等价关系。

设$R$是$\Sigma^{ * } $上的等价关系，则称$|\Sigma^{ * } /R|$是$R$关于$\Sigma^{ * } $的指数（index）（也就是一个集合的等价类的个数），简称为$R$的指数。$\Sigma^{ * } $关于$R$的一个等价类，也就是$\Sigma^{ * } /R$的任意一个元素，简称为$R$的一个等价类。

由于$xR_My\Rightarrow xR_{L(M)}y$，可以证明对于任意DFA：$M=(Q,\Sigma,\delta,q_0,F)$都有$|\Sigma^{ * } /R_{L(M)}|\leq|\Sigma^{ * } /R_M|\leq|Q|$。同时可以看出$R_M$对$\Sigma^{ * } $的划分比$R_{L(M)}$更加“细”，$R_M$可以将$R_{L(M)}$所划分的等价类进一步划分，称$R_M$是$R_{L(M)}$的加细（refinement）。

Myhill-Nerode定理：有三个等价的命题：

$L\subseteq\Sigma^{ * } $是RL。
$L$是$\Sigma^{ * } $上的某个具有有穷指数的右不变等价关系$R$的某些等价类的并。
$R_L$具有有穷指数。

证明：不妨证明从（1）到（2）、从（2）到（3）、从（3）到（1）都是成立的。

从（1）到（2）：

由于$L$是RL，存在识别它的DFA：$M=(Q,\Sigma,\delta,q_0,F)$，由于$R_M$是$\Sigma^{ * } $上的右不变的等价关系，同时$|\Sigma^{ * } |\leq|Q|$，故$R_M$有有穷指数，$R_M$即为满足要求的一个右不变等价关系。

从（2）到（3）：

设$L$是$\Sigma^{ * } $上具有有穷指数的右不变等价关系$R$的某些等价类的并，不妨证明$R$是$R_L$的加细，也就是证明$\forall x,y\in\Sigma^{ * } ,xRy\Rightarrow xR_Ly$。由于$R$的右不变性，可知对于$\forall z\in\Sigma^{ * } $都有$xzRyz$，而$L$又是$R$的某些等价类的并，所以$xz\in L\Leftrightarrow yz\in L$，也就是说$xR_Ly$。

从（3）到（1）：

设$R_L$有有穷指数，构造DFA：$M’=(\Sigma^{ * } /R_L,\Sigma,\delta’,[\epsilon],${$[x]|x\in L$}$)$，其中$[\epsilon]$表示$\epsilon$所在的等价类所对应的状态，$[x]$表示$x$所在的等价类所对应的状态。对于任意$([x],a)\in(\Sigma^{ * } /R_L)\times\Sigma$都有$\delta’([x],a)=[xa]$，那么有$L(M’)=L$，这里构造的$M’$称为最小DFA。

由Myhill-Nerode定理可以得到两个推论，在此不对两个推论作出证明：

$L$是RL，识别它的DFA：$M=(Q,\Sigma,\delta,q_0,F)$，则$|\Sigma^{ * } /R_L|\leq|Q|$。

$L$是RL，在同构意义下，接受$L$的最小DFA是唯一的。

定理得到证明，这个定理可以用于证明一个语言是RL，也可以证明一个语言不是RL。例如语言{$0^n1^n|n\geq 0$}，可以发现它的等价关系$R_L$的指数是无穷的，因此$L$不是RL。

DFA的极小化

设DFA：$M=(Q,\Sigma,\delta,q_0,F)$，如果$\exists x\in\Sigma^{ * } $使得$Q$中的两个状态$q$和$p$，在$\delta(q,x)\in F$和$\delta(p,x)\in F$中有且仅有一个成立，则称$q$和$p$是可以区分的（distinguishable）；否则称$q$和$p$等价，记作$q\equiv p$。

为了让DFA极小化，实际上只需要找到一个DFA中全部的可区分状态对，再将不可区分的状态对合并为一个状态，同时保留被合并的状态到其他的状态的转移箭头，同时去掉DFA中的不可达状态，就得到了最小DFA。

DFA的极小化示例

正则语言的泵引理

正则语言的泵引理是如此的重要和有影响力，以至于人们一直将其称为引理而未改称其为定理。正则语言的泵引理是它的一种特殊性质：语言中的所有字符串只要它的长度不小于某个特定值————泵长度（pumping length），就可以被“抽取”，也就是说字符串中有一段字串，无论字串重复多少次，得到的字符串依旧在这个语言里。下面给出其形式化表述和相应证明：

泵引理（pumping lemma）：若$L$是一个RL，则存在一个正整数$N$，对$w\in L$，只要$|w|>N$，就可以将$w$分为三部分$w=xyz$使得：

$y\neq\epsilon$
$|xy|\leq N$
$\forall k\geq 0,xy^kz\in L$

证明：设$M=(Q,\Sigma,\delta,q_0,F)$识别语言$L$，其中$|Q|=N$，在读入长度为$m$的串时（$m\geq N$），它所经过的状态有$q_0,q_1,\cdots,q_m$，根据鸽巢原理，必然有两个状态是相同的，不妨设$q_i=q_j,0\leq i< j\leq N$，那么可以划分$w$为$x=a_1a_2 \cdots a_i,y=a_{i+1}\cdots a_j,z=a_{i+1} \cdots a_M$，找到了这样一种划分符合泵引理的要求，证毕。

有了泵引理后，可以发现并不是所有语言都是RL，例如{$0^n1^n|n\geq 0$}这样一个语言便不是一个RL，它不满足泵引理的条件。

但是值得注意的是泵引理是某个语言是RL的必要条件而不是充分条件，例如{$0^i1^j2^k|i,j,k\geq 0,并且若i=1,则j=k$}，记这个语言为$F$，考虑语言$L=L(01^{ * }2^{ * })$，那么$L\cap F=${$01^n2^n|n\geq 0$}，很明显后者不是RL，由于RL在交运算下封闭，所以$F$不是RL，但它满足泵引理。

八、正则语言的判定性质

任何语言都有3个经典的判定问题：

以某种形式化模型描述的语言是否为空？是否无穷？
某个特定的串$w$是否属于所描述的语言？
以两种方式描述的语言，是否是相同的？

下面给出了这三个问题的相关回答：

设DFA：$M=(Q,\Sigma,\delta,q_0,F)$

那么$L=L(M)$非空的充分必要条件是：存在$x\in\Sigma^{ * } ,|x|<|Q|,\hat{\delta}(q_0,x)\in F$。

$L=L(M)$无穷的充分必要条件是：存在$x\in\Sigma^{ * } ,|Q|\leq|x|<2|Q|,\hat{\delta}(q_0,x)\in F$。

设DFA：$M_1=(Q_1,\Sigma,\delta_1,q_1,F_1),M_2=(Q_2,\Sigma,\delta_2,q_2,F_2)$，则存在判断$L(M_1),L(M_2)$是否相同的算法。

记$L_1=L(M_1),L_2=L(M_2)$，那么$(L_1\cap\overline{L_2})\cup(\overline{L_1}\cap L_2)$是正则的，可以被某个有穷自动机$M_3$接受，而$M_3$接受某个串当且仅当$L_1\neq L_2$，已经证明了存在算法判断$L(M_3)$是否为空，得证。

设$L$是字母表$\Sigma$上的RL，对于任意的$w\in\Sigma^{ * } $，存在判定$w$是否为$L$的句子的算法。

由于$L$是RL，故存在DFA使得它接受这个语言。